Introduction
This vignette compares outputs from the ADMB model to the RTMB model
within the sbt package. This is done using a fixed
parameter run and then by optimising. In the fixed parameter run the
parameter values from a single cell of the ADMB model are used as fixed
value inputs to sbt and outputs from sbt are
generated then compared to the ADMB outputs.
Fixed parameter run
Comparison table
The table below includes transformed parameters (i.e., in natural space), derived quantities, priors, penalties, likelihoods, and objective function values for the ADMB model, the RTMB model, and the difference and percent difference between the two models:
| ADMB | RTMB | Difference | Percent difference | |
|---|---|---|---|---|
| Parameters | ||||
| B0 | 1.08358e+07 | 1.083578e+07 | 18.0862526 | 0.0002 |
| psi | 1.50000e+00 | 1.500000e+00 | 0.0000000 | 0.0000 |
| sigmaR | 6.00000e-01 | 6.000000e-01 | 0.0000000 | 0.0000 |
| h | 5.50000e-01 | 5.500000e-01 | 0.0000000 | 0.0000 |
| q HSP | 1.00000e+00 | 1.000000e+00 | 0.0000000 | 0.0000 |
| m0 | 4.00000e-01 | 4.000000e-01 | 0.0000000 | 0.0000 |
| m4 | 1.67050e-01 | 1.670507e-01 | -0.0000007 | 0.0004 |
| m10 | 6.50000e-02 | 6.500000e-02 | 0.0000000 | 0.0000 |
| m30 | 4.57410e-01 | 4.574100e-01 | 0.0000000 | 0.0000 |
| Derived quantities | ||||
| R0 | 8.74439e+06 | 8.744386e+06 | 3.9612256 | 0.0000 |
| alpha | 1.09929e+07 | 1.099294e+07 | -42.4487450 | 0.0004 |
| beta | 2.78634e+06 | 2.786344e+06 | -3.9206779 | 0.0001 |
| tau_ac2 | 6.44716e-01 | 6.447156e-01 | 0.0000004 | 0.0001 |
| Priors & penalties | ||||
| kludge | 0.00000e+00 | 0.000000e+00 | 0.0000000 | 0.0000 |
| sel.change | 7.06247e+01 | 7.062467e+01 | 0.0000305 | 0.0000 |
| sel.smooth | 3.42249e+01 | 3.422494e+01 | -0.0000408 | 0.0001 |
| rec | -3.03390e+01 | -3.033900e+01 | 0.0000045 | 0.0000 |
| m0 | 0.00000e+00 | 0.000000e+00 | 0.0000000 | 0.0000 |
| m10 | 0.00000e+00 | 0.000000e+00 | 0.0000000 | 0.0000 |
| steep | 0.00000e+00 | 0.000000e+00 | 0.0000000 | 0.0000 |
| omega | 0.00000e+00 | 0.000000e+00 | 0.0000000 | 0.0000 |
| expl | 0.00000e+00 | 0.000000e+00 | 0.0000000 | 0.0000 |
| sel.init | 2.00000e-07 | 2.000000e-07 | 0.0000000 | 0.0002 |
| hstar | 7.63360e+00 | 7.633597e+00 | 0.0000030 | 0.0000 |
| Likelihoods & objective function | ||||
| LL1 | 1.94607e+02 | 1.946072e+02 | -0.0002198 | 0.0001 |
| LL2 | 3.09202e+01 | 3.092031e+01 | -0.0001054 | 0.0003 |
| LL3 | 3.48981e+01 | 3.489813e+01 | -0.0000286 | 0.0001 |
| LL4 | 3.82627e+01 | 3.826276e+01 | -0.0000591 | 0.0002 |
| Indo | 9.30514e+01 | 9.305138e+01 | 0.0000202 | 0.0000 |
| Aus | 4.54265e+01 | 4.542650e+01 | -0.0000019 | 0.0000 |
| CPUE | -6.46131e+01 | -6.461295e+01 | -0.0001494 | 0.0002 |
| Tags | 1.76553e+02 | 1.765530e+02 | 0.0000081 | 0.0000 |
| Aerial | 3.98139e+00 | 3.981441e+00 | -0.0000505 | 0.0013 |
| Troll | -1.20015e+01 | -1.200157e+01 | 0.0000656 | 0.0005 |
| POP | 1.75465e+03 | 1.754654e+03 | -0.0037102 | 0.0002 |
| HSP | 2.19884e+03 | 2.199118e+03 | -0.2776306 | 0.0126 |
| GT | 1.45904e+03 | 1.459035e+03 | 0.0046028 | 0.0003 |
| ObjF | 6.03576e+03 | 6.036037e+03 | -0.2771518 | 0.0046 |
Comparison figures
The following figures compare outputs from the ADMB and RTMB models:
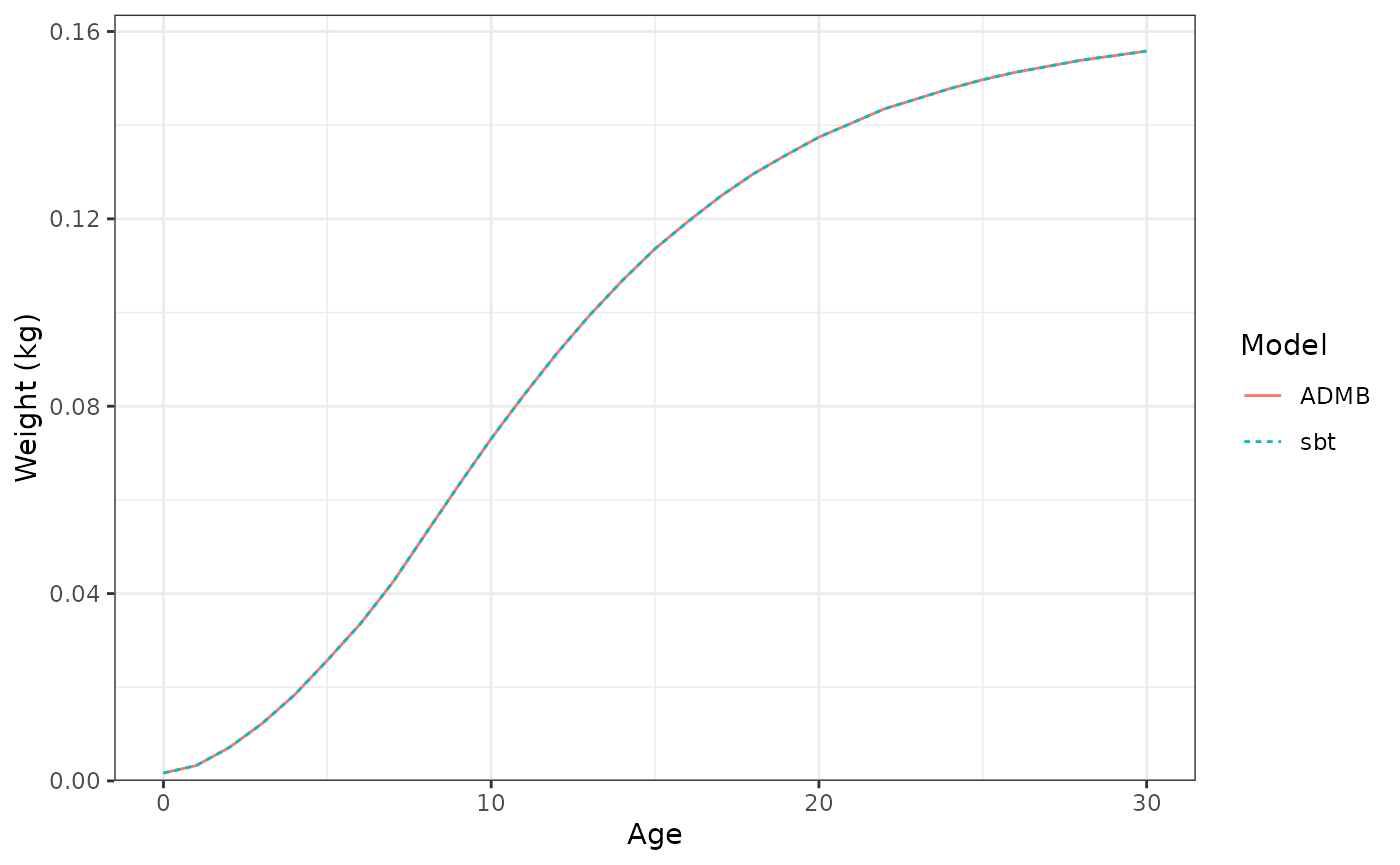
Average weight (kg) at age.
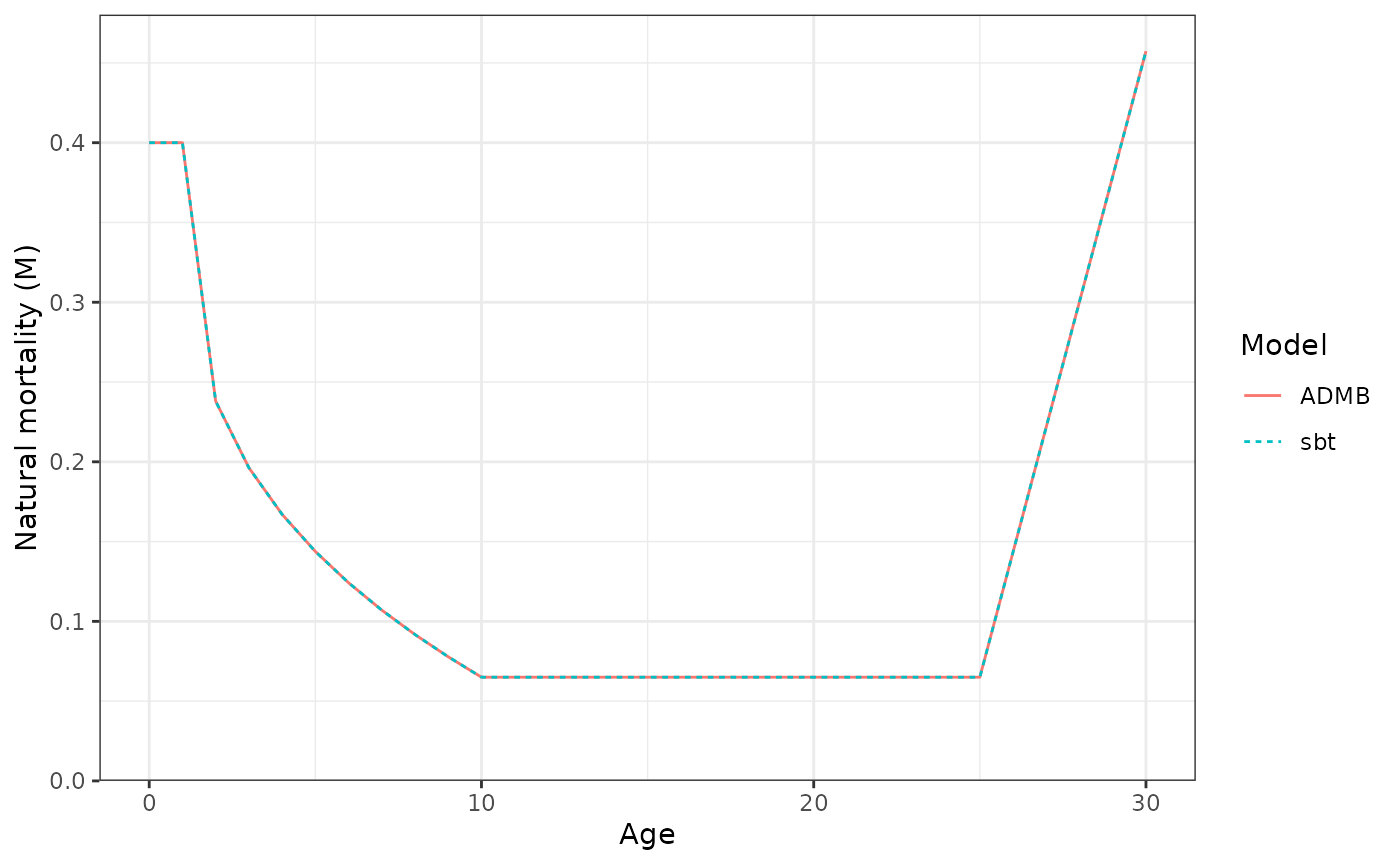
Natural mortality (M) at age.
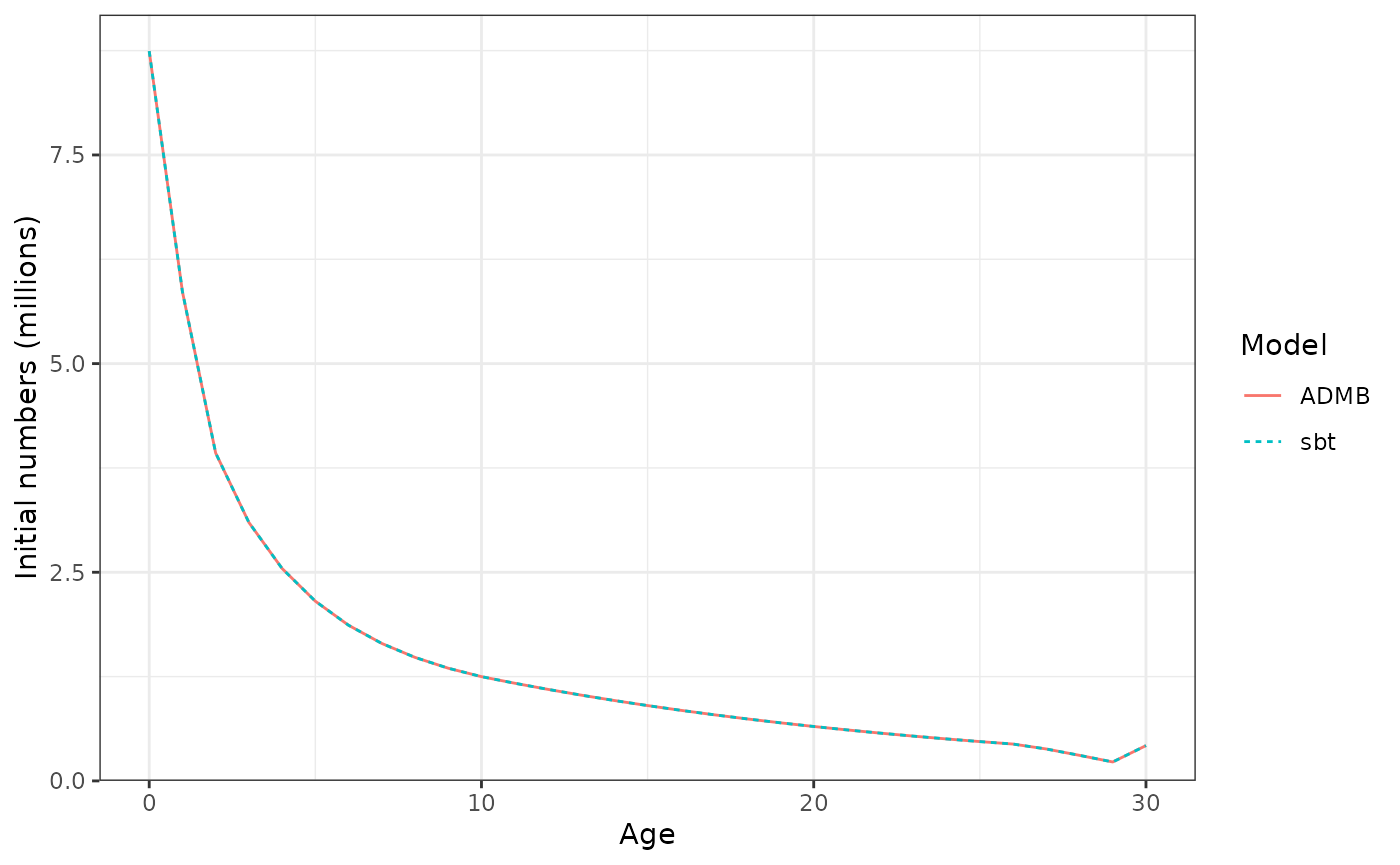
Initial numbers at age in the population.
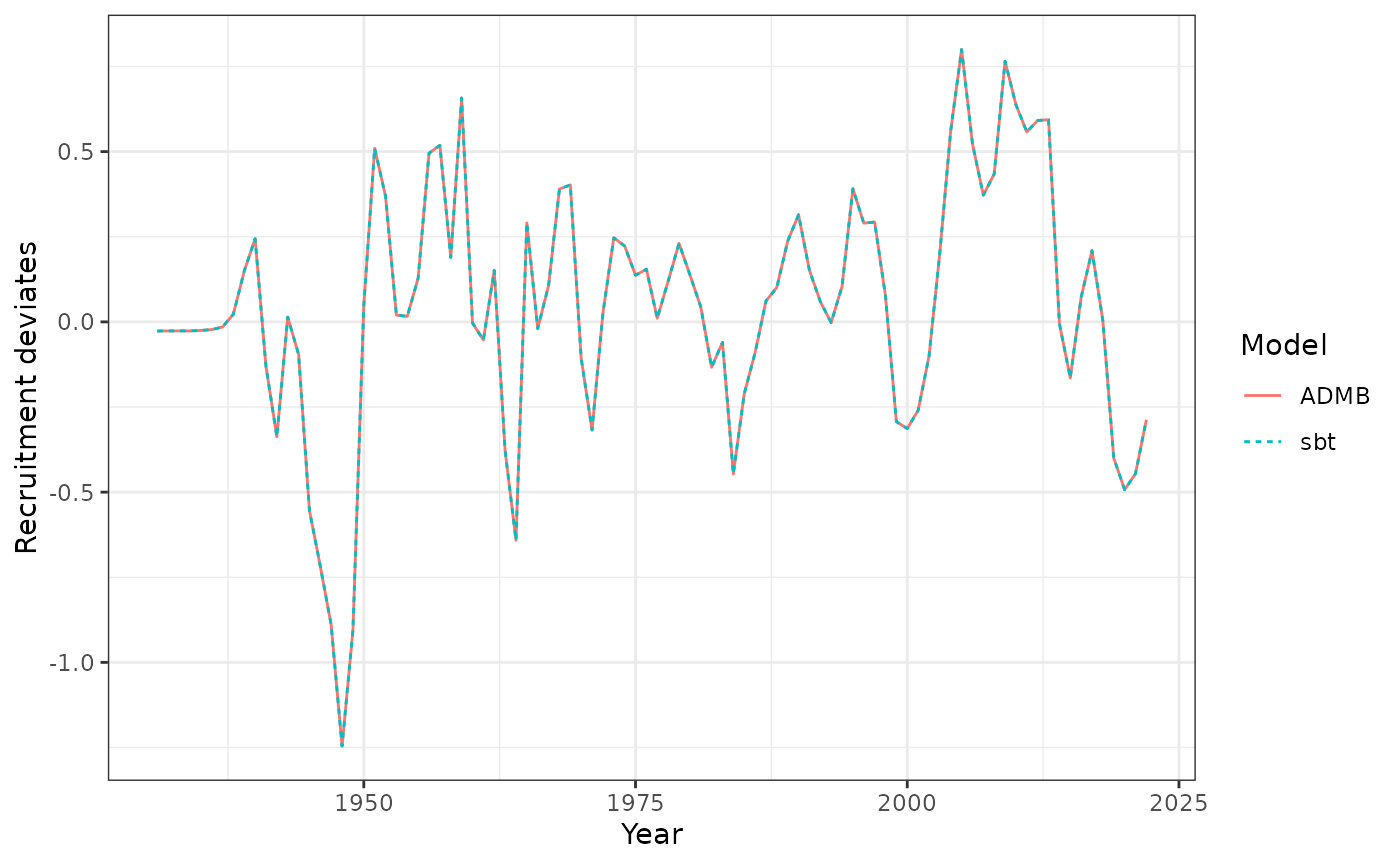
Recruitment deviates each year.
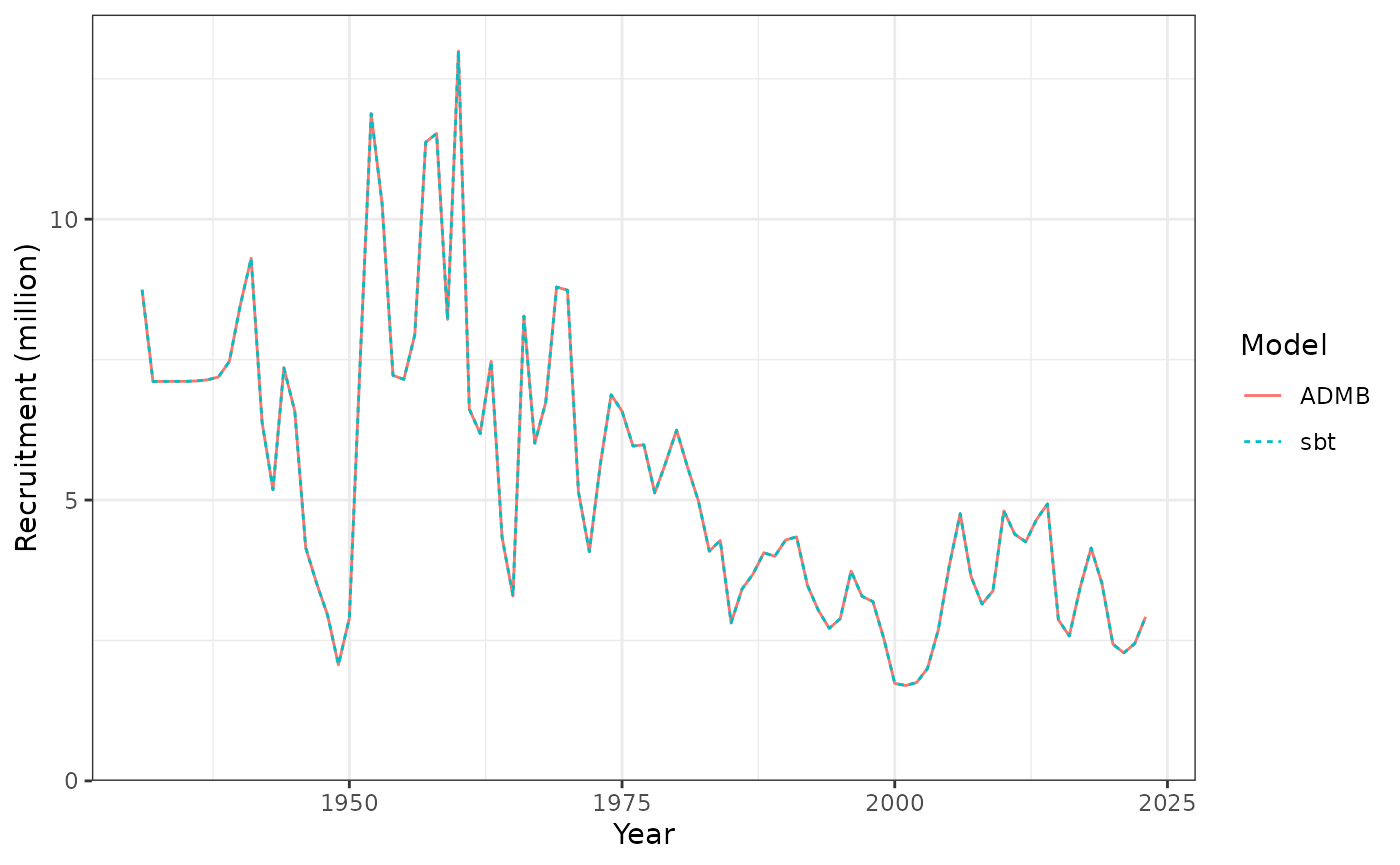
Recruitment each year.
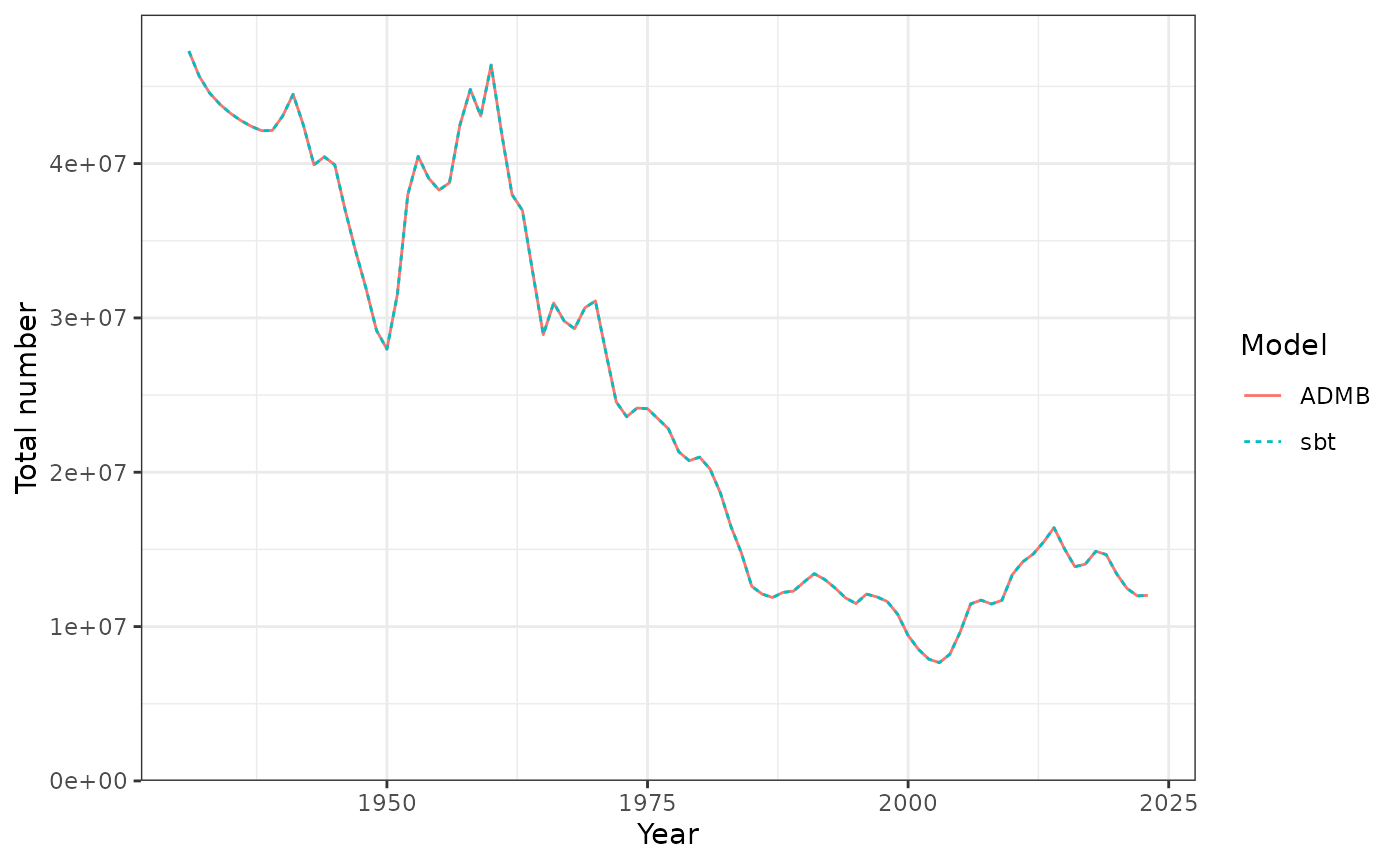
Total number of inidividuals each year.
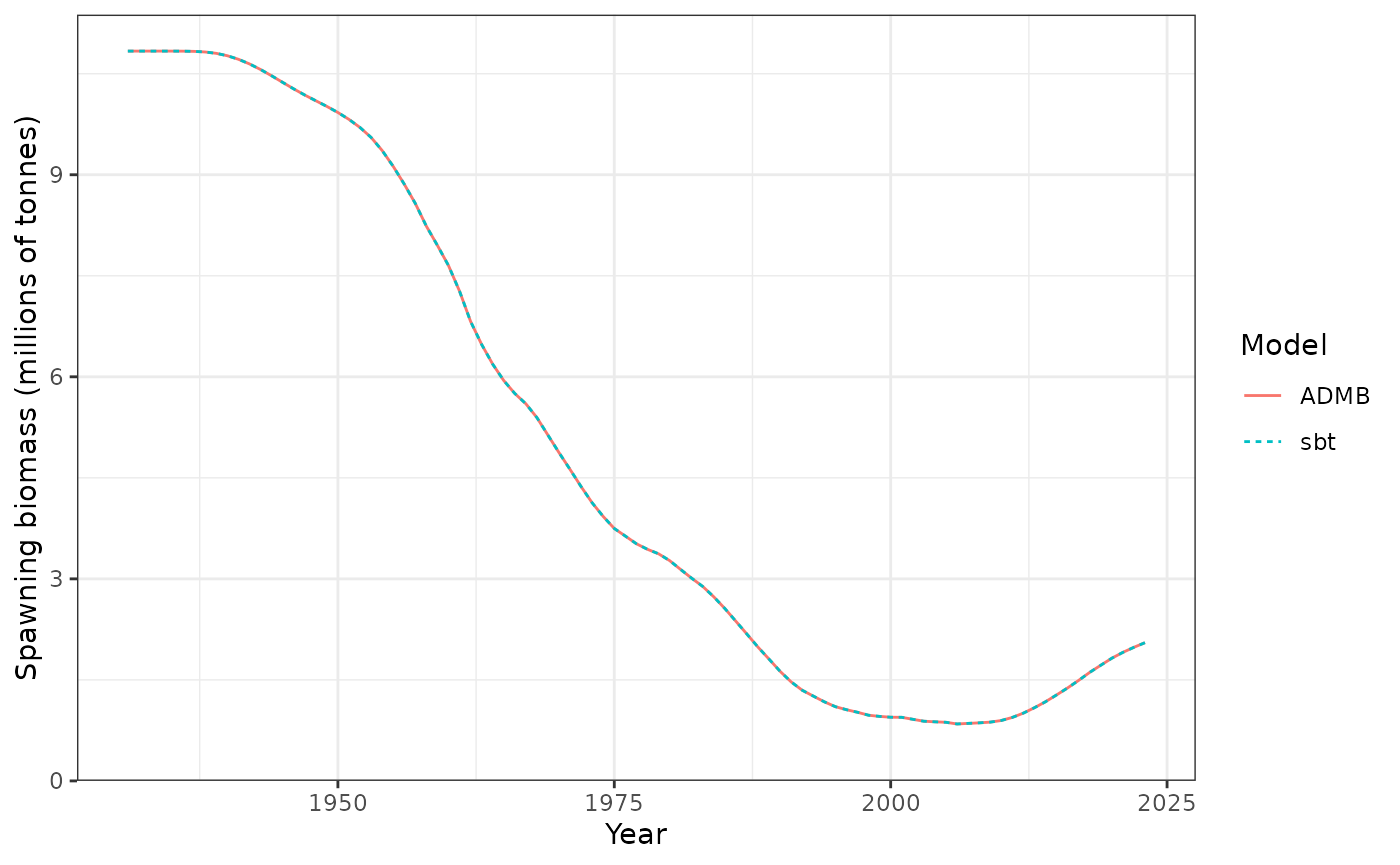
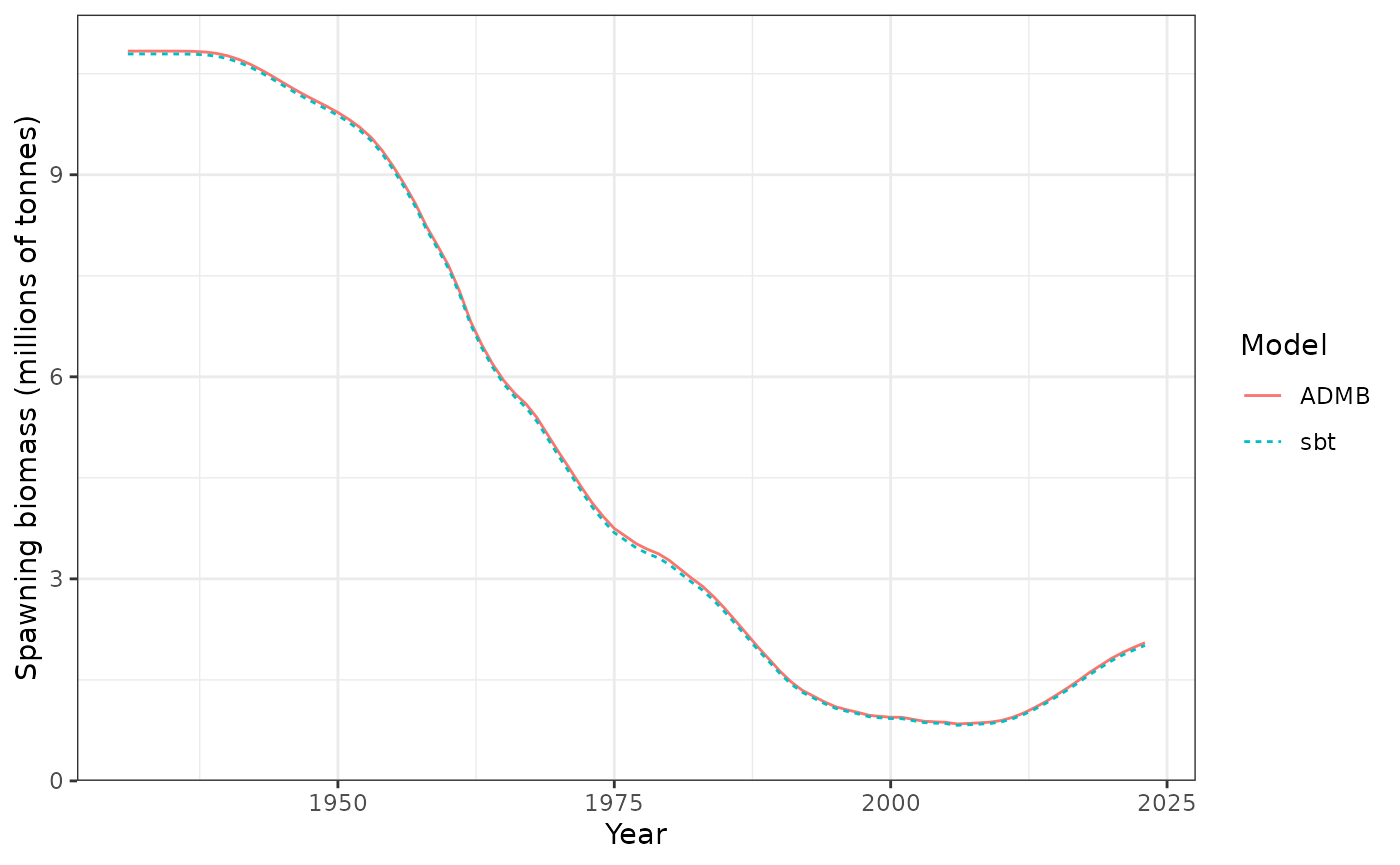
Spawning biomass (tonnes).
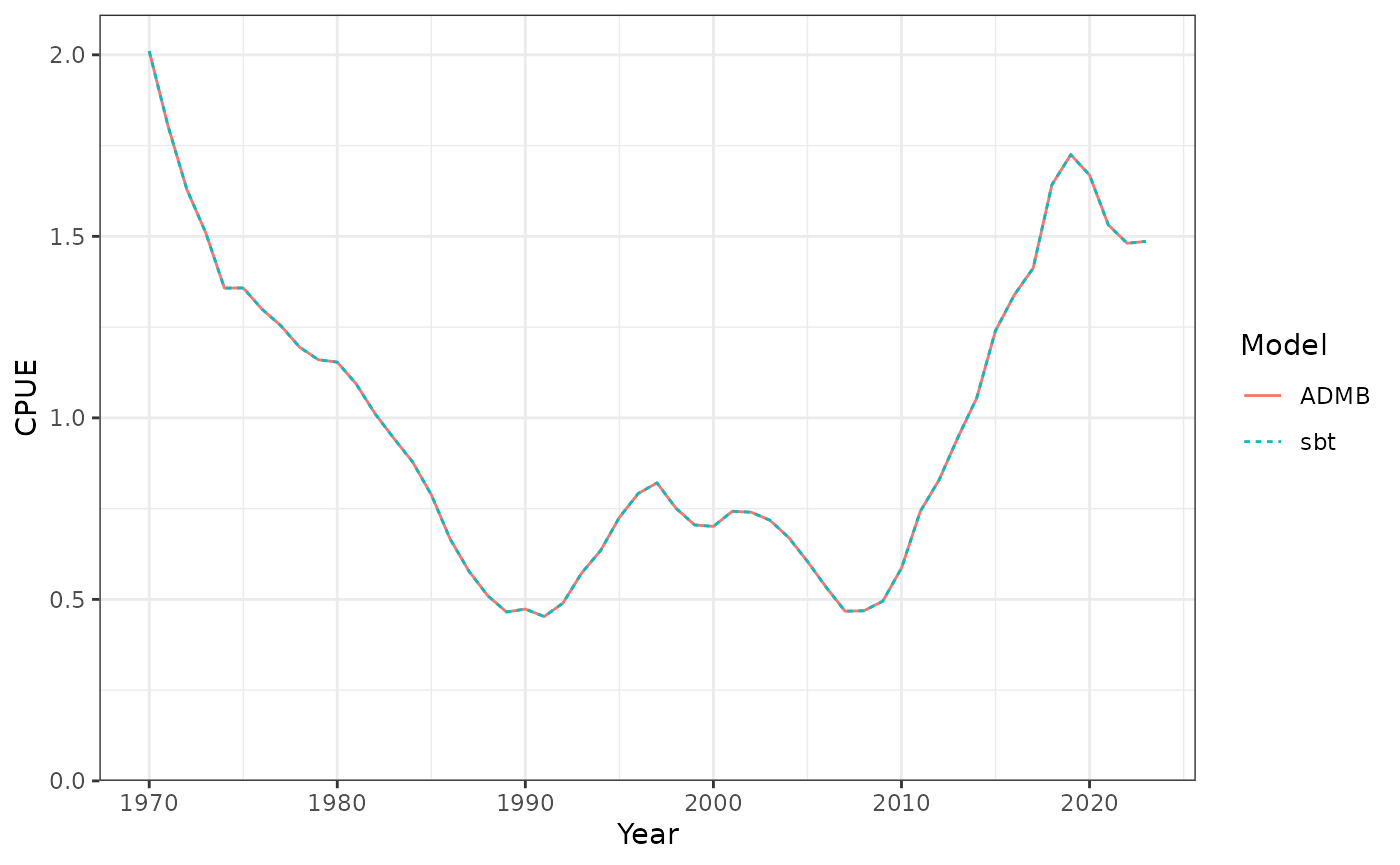
Catch per unit effort (CPUE).
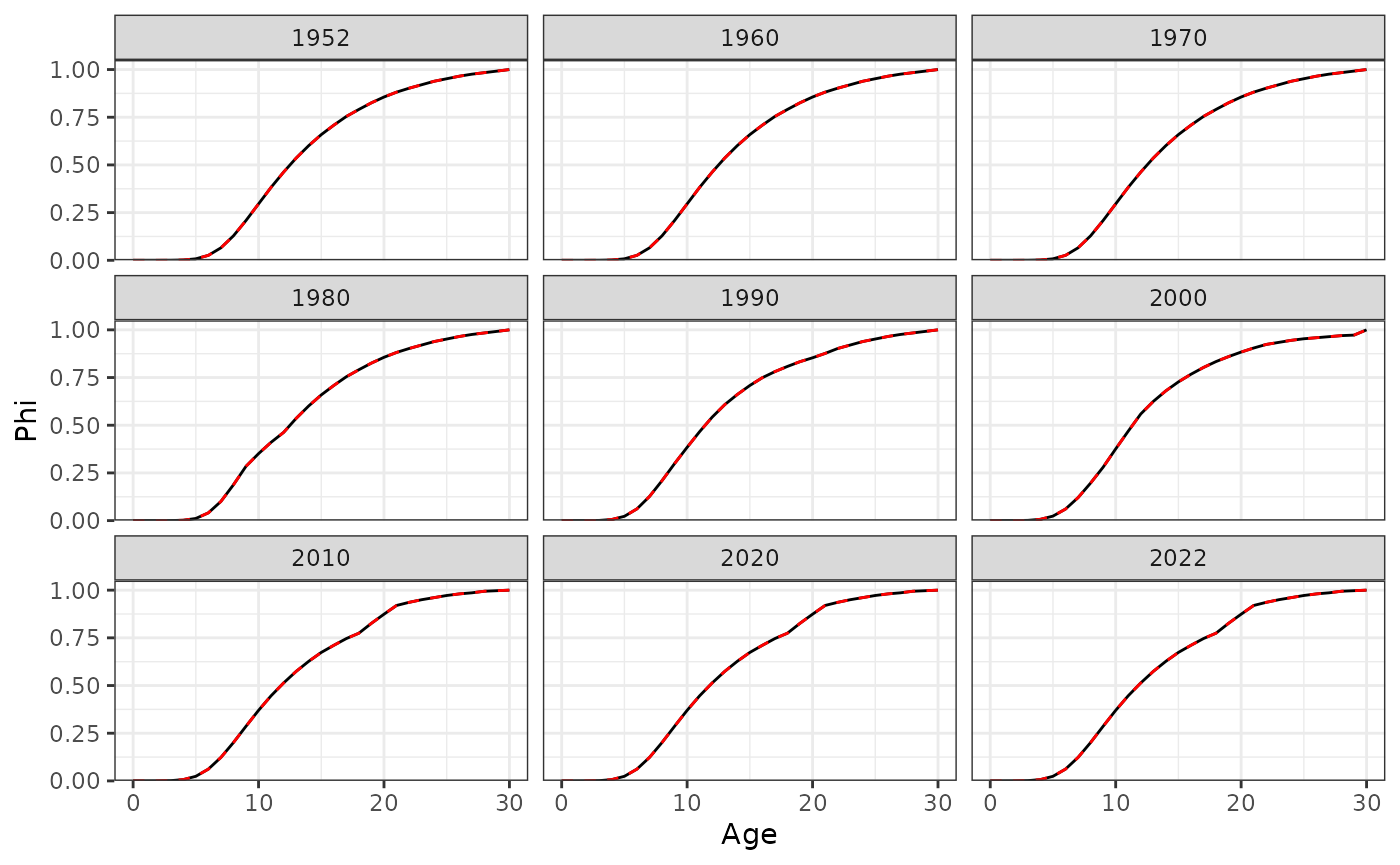
Phi at age for a subset of years.
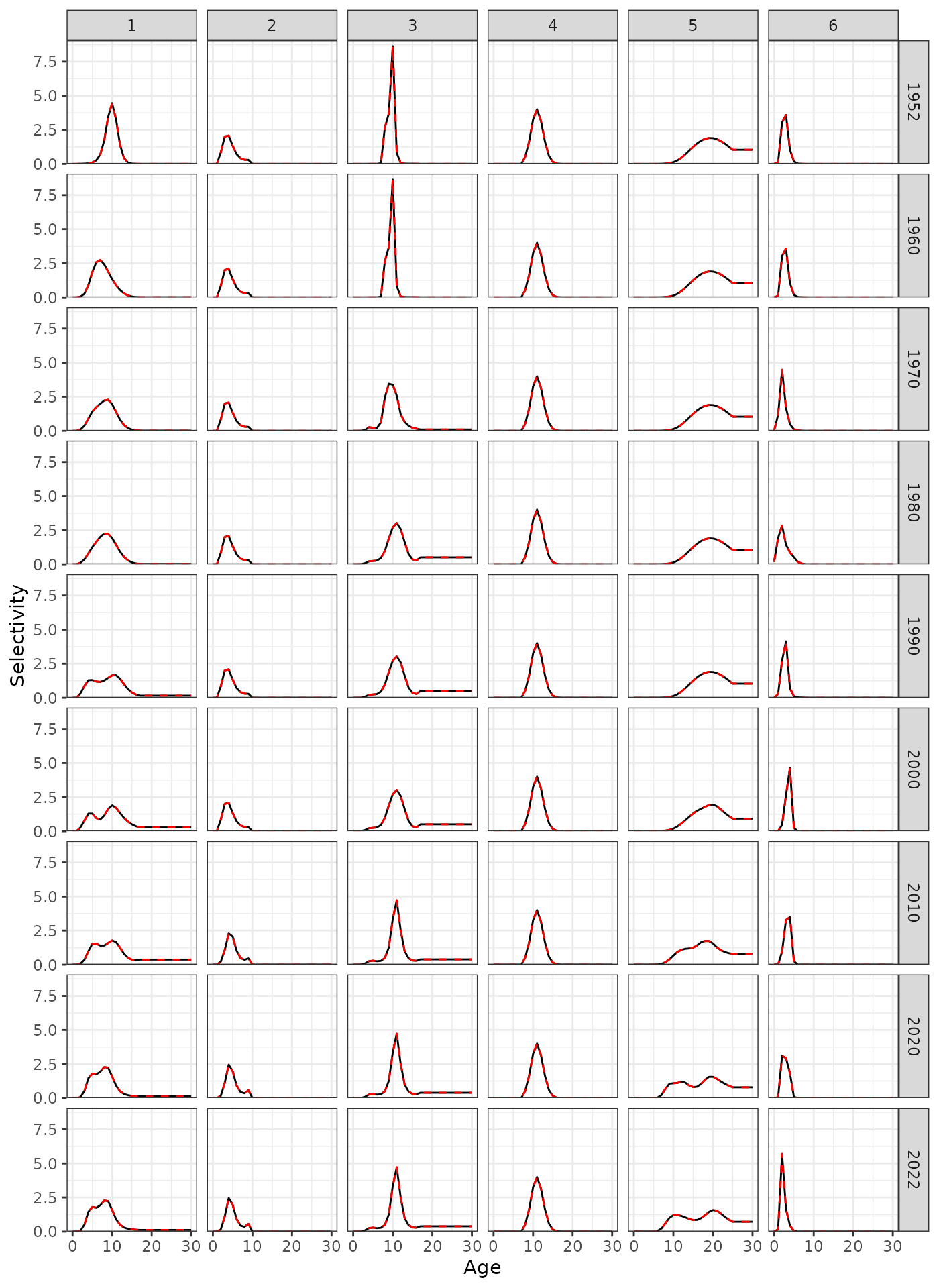
Selectivity at age for a subset of years.
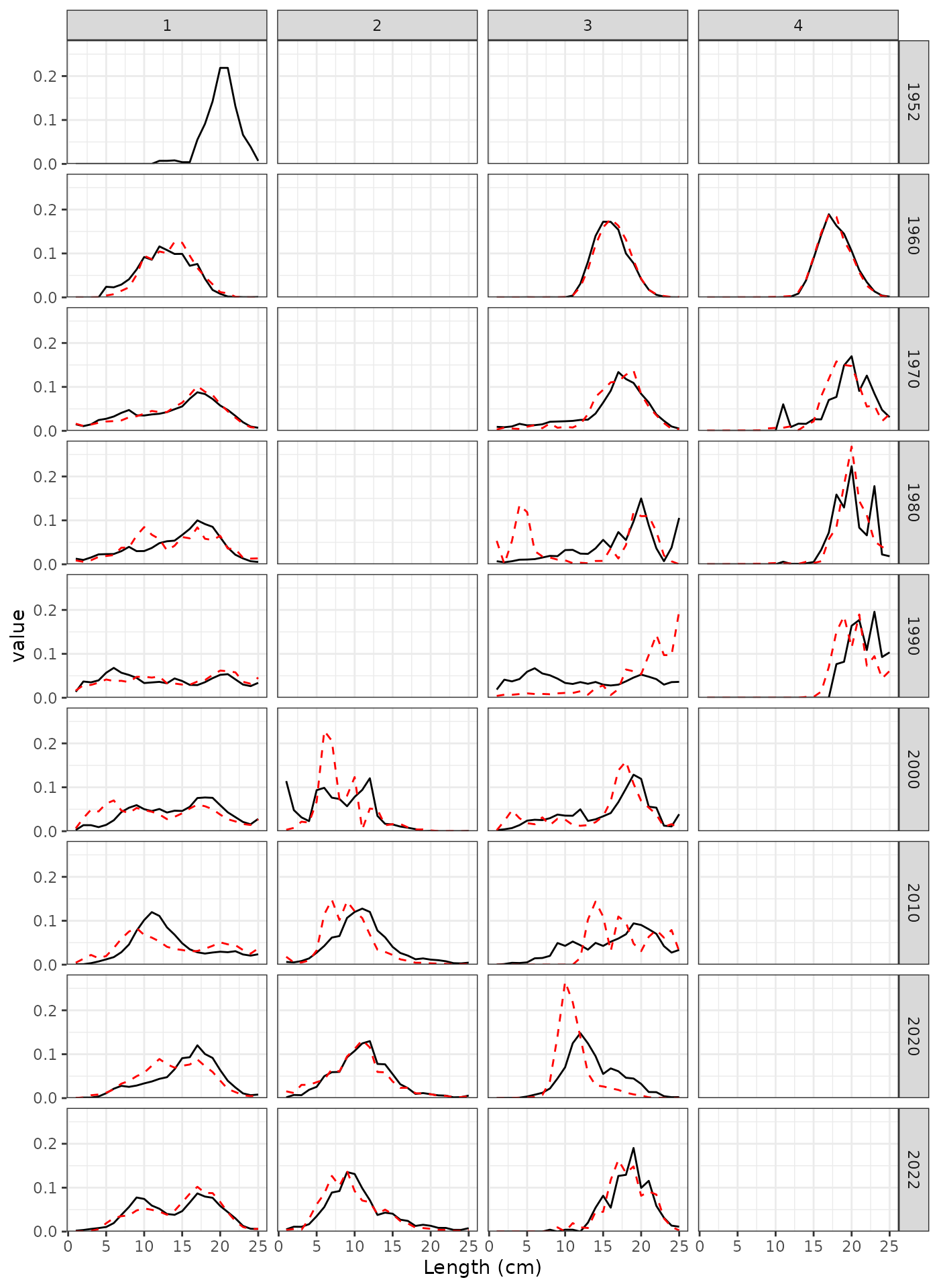
LF observations for a subset of years.
#> [1] NA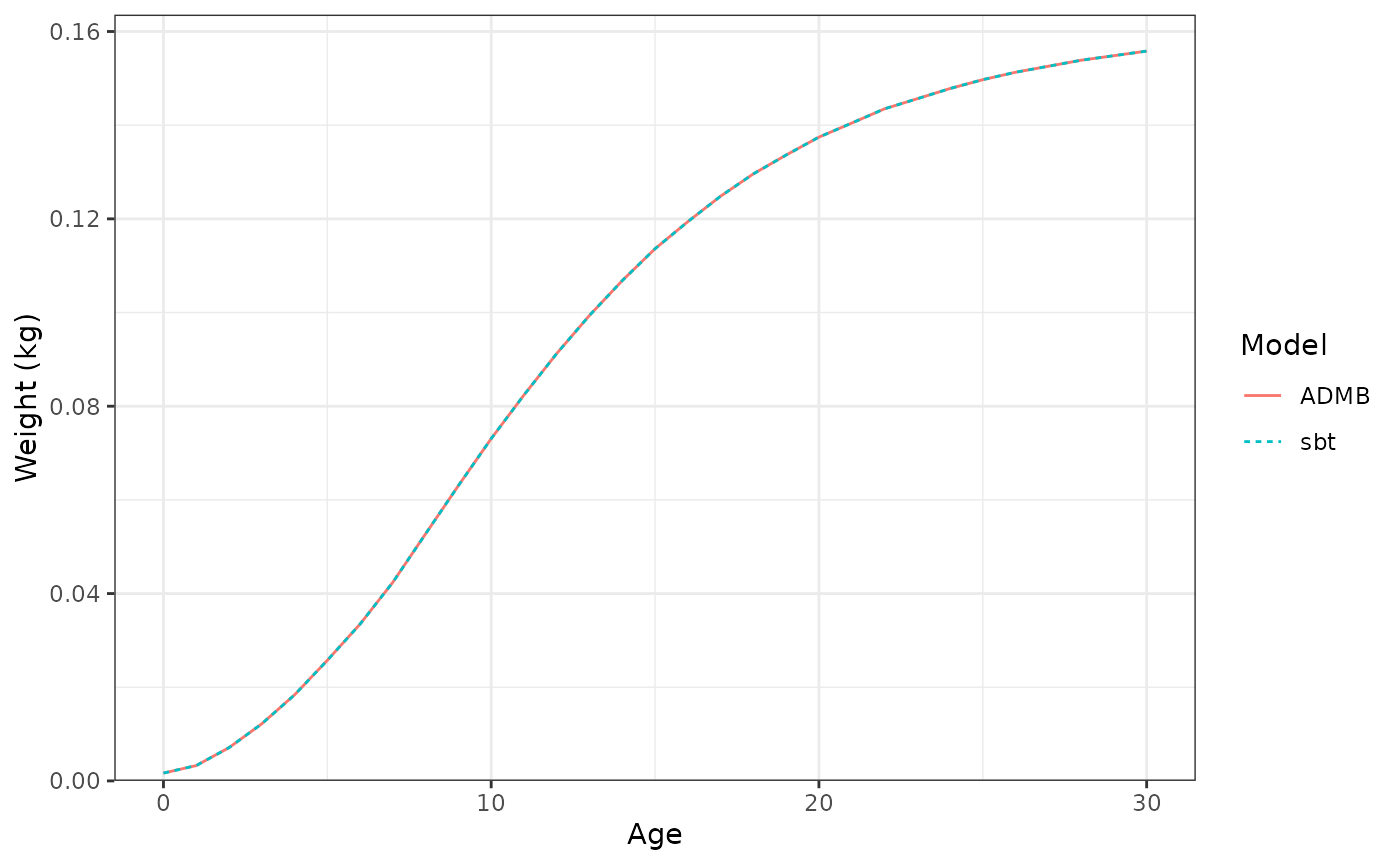
AF observations for a subset of years.
#> [1] NA NA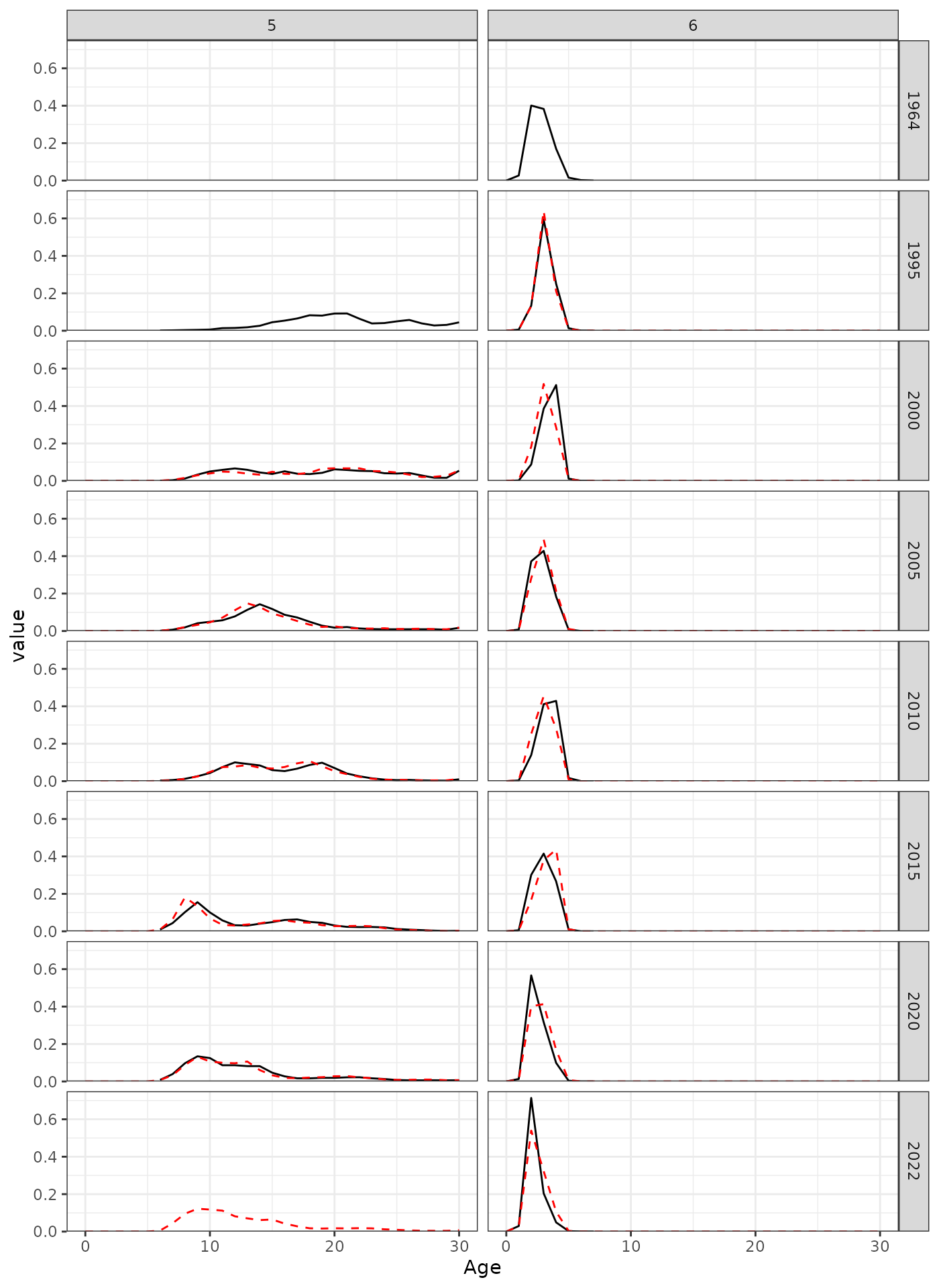
AF predictions for a subset of years.