The sbt model • sbt

Introduction

The sbt software is an R package (R Core Team 2024) that contains the CCSBT operating model (OM) coded using RTMB Kristensen (2024). This page provides an example of using the sbt model.

Load inputs

The sbt RTMB model is loaded along with several R functions using library(sbt). The kableExtra package is used for generating tables of inputs. The tidyverse package is used for data manipulation and plotting. The code theme_set(theme_bw()) alters the plot aesthetics.

# remotes::install_github("janoleko/RTMBdist")
# remotes::install_github("andrjohns/StanEstimators")
# remotes::install_github("Cole-Monnahan-NOAA/adnuts")
library(kableExtra)
library(tidyverse)
library(sbt)

theme_set(theme_bw())

Below are example inputs that are loaded from the sbt package. Normally the user would import these inputs (e.g., from .csv files using the read_csv function).

# names(data_csv1)
# names(data_par1)
# names(data_labrep1)

The data list is defined below and then the get_data function is used to set up some additional inputs that are required before the data list can be passed to MakeADFun.

data <- list(
  last_yr = 2022, age_increase_M = 25, length_m50 = 150, length_m95 = 180, 
  catch_UR_on = 0, catch_surf_case = 1, catch_LL1_case = 1, 
  scenarios_surf = data_csv1$scenarios_surface, 
  scenarios_LL1 = data_csv1$scenarios_LL1,
  removal_switch_f = c(0, 0, 0, 1, 0, 0), # 0=harvest rate, 1=direct removals
  sel_min_age_f = c(2, 2, 2, 8, 6, 0, 2),
  sel_max_age_f = c(17, 9, 17, 22, 25, 7, 17),
  sel_end_f = c(1, 0, 1, 1, 1, 0, 1),
  sel_LL1_yrs = c(1952, 1957, 1961, 1965, 1969, 1973, 1977, 1981, 1985, 1989, 
                  1993, 1997, 2001, 2006, 2007, 2008, 2011, 2014, 2017, 2020),
  sel_LL2_yrs = c(1969, 2001, 2005, 2008, 2011, 2014, 2017, 2020),
  sel_LL3_yrs = c(1954, 1961, 1965, 1969, 1970, 1971, 2005, 2006, 2007),
  sel_LL4_yrs = c(1953),
  sel_Ind_yrs = c(1976, 1995, 1997, 1999, 2002, 2004, 2006, 2008, 2010, 2012, 
                  2013, 2014, 2015, 2016, 2017, 2018, 2019, 2020, 2021, 2022),
  sel_Aus_yrs = c(1952, 1969, 1973, 1977, 1981, 1985, 1989, 1993, 1997, 1998, 
                  1999, 2000, 2001, 2002, 2003, 2004, 2005, 2006, 2007, 2008, 
                  2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 
                  2019, 2020, 2021, 2022),
  sel_CPUE_yrs = c(1969, 1973, 1977, 1981, 1985, 1989, 1993, 1997, 2001, 2006, 
                   2007, 2008, 2011, 2014, 2017, 2020),
  af_switch = 9,
  lf_switch = 9, lf_minbin = c(1, 1, 1, 11),
  cpue_switch = 1, cpue_a1 = 5, cpue_a2 = 17,
  troll_switch = 1, 
  aerial_switch = 4, aerial_tau = 0.3,
  tag_switch = 1, tag_var_factor = 1.82,
  hsp_switch = 1, hsp_false_negative = 0.7467647, 
  pop_switch = 1, 
  gt_switch = 1
)

data <- get_data(data_in = data)

names(data)
#>  [1] "last_yr"             "age_increase_M"      "length_m50"         
#>  [4] "length_m95"          "removal_switch_f"    "sel_min_age_f"      
#>  [7] "sel_max_age_f"       "sel_end_f"           "af_switch"          
#> [10] "lf_switch"           "lf_minbin"           "cpue_switch"        
#> [13] "cpue_a1"             "cpue_a2"             "troll_switch"       
#> [16] "aerial_switch"       "aerial_tau"          "tag_switch"         
#> [19] "tag_var_factor"      "hsp_switch"          "hsp_false_negative" 
#> [22] "pop_switch"          "gt_switch"           "first_yr"           
#> [25] "n_year"              "n_season"            "min_age"            
#> [28] "max_age"             "n_age"               "n_length"           
#> [31] "n_fishery"           "age_a"               "length_mu_ysa"      
#> [34] "length_sd_a"         "weight_fya"          "first_yr_catch"     
#> [37] "first_yr_catch_f"    "n_catch"             "catch_year"         
#> [40] "catch_obs_ysf"       "sel_change_year_fy"  "pop_obs"            
#> [43] "paly"                "hsp_obs"             "gt_obs"             
#> [46] "gt_nscan"            "gt_nrec"             "aerial_years"       
#> [49] "aerial_obs"          "aerial_cv"           "aerial_cov"         
#> [52] "troll_years"         "troll_obs"           "troll_sd"           
#> [55] "cpue_years"          "cpue_obs"            "cpue_sd"            
#> [58] "af_min_age"          "af_max_age"          "n_af"               
#> [61] "af_year"             "af_fishery"          "af_obs"             
#> [64] "af_n"                "dl_yal"              "alk_ysal"           
#> [67] "lf_year"             "lf_fishery"          "lf_season"          
#> [70] "lf_obs"              "lf_n"                "lf_slices"          
#> [73] "af_sliced"           "af_sliced_ysfa"      "cpue_lfs"           
#> [76] "cpue_n"              "tag_shed_immediate"  "tag_shed_continuous"
#> [79] "tag_rep_rates_ya"    "tag_rel_min_age"     "tag_rel_max_age"    
#> [82] "tag_release_cta"     "tag_recap_ctaa"      "tag_recap_max_age"  
#> [85] "min_K"               "n_K"                 "n_T"                
#> [88] "n_I"                 "n_J"

Input tables

Below are examples of some of the model inputs in tabular form.

Mean length (cm) by year, season, and age. Only a subset of years and ages 1-10 are shown:

kbl(bind_rows(head(length_mean), tail(length_mean))[,1:13]) %>%
  add_header_above(c(" " = 2, "Age" = 11))

		Age
Year	Season	0	1	2	3	4	5	6	7	8	9	10
1931	1	45	57.1	74.1	88.8	101.8	113.9	124.3	133.3	141.0	147.6	153.3
1932	1	45	57.1	74.1	88.8	101.8	113.9	124.3	133.3	141.0	147.6	153.3
1933	1	45	57.1	74.1	88.8	101.8	113.9	124.3	133.3	141.0	147.6	153.3
1934	1	45	57.1	74.1	88.8	101.8	113.9	124.3	133.3	141.0	147.6	153.3
1935	1	45	57.1	74.1	88.8	101.8	113.9	124.3	133.3	141.0	147.6	153.3
1936	1	45	57.1	74.1	88.8	101.8	113.9	124.3	133.3	141.0	147.6	153.3
2017	2	50	68.9	91.6	105.5	117.3	127.2	135.6	142.7	148.7	153.8	158.1
2018	2	50	68.9	91.6	105.5	117.3	127.2	135.6	142.7	148.7	153.8	158.1
2019	2	50	68.9	91.6	105.5	117.3	127.2	135.6	142.7	148.7	153.8	158.1
2020	2	50	68.9	91.6	105.5	117.3	127.2	135.6	142.7	148.7	153.8	158.1
2021	2	50	68.9	91.6	105.5	117.3	127.2	135.6	142.7	148.7	153.8	158.1
2022	2	50	68.9	91.6	105.5	117.3	127.2	135.6	142.7	148.7	153.8	158.1

The parent offspring pair (POP) data set:

kbl(tail(POPs, 15))

Cohort	CaptureYear	CaptureCov	CaptureSwitch	Comps
2007	2012	15	1	1315
2008	2012	15	1	963
2009	2012	15	1	876
2010	2012	15	1	903
2011	2012	15	1	899
2003	2013	15	1	1317
2004	2013	15	1	1325
2005	2013	15	1	1356
2006	2013	15	1	1347
2007	2013	15	1	1315
2008	2013	15	1	963
2009	2013	15	1	876
2010	2013	15	1	903
2011	2013	15	1	899
2012	2013	15	1	953

The unaccounted catch (tonnes) data set:

kbl(tail(catch_UA, 15))

Year	LL1	LL2	LL3	LL4	Indonesia	Australia
2008	72	0	0	0	0	0
2009	152	0	0	0	0	0
2010	271	0	0	0	0	0
2011	151	0	0	0	0	0
2012	275	0	0	0	0	0
2013	432	0	0	0	0	0
2014	121	0	0	0	0	0
2015	326	0	0	0	0	0
2016	756	0	0	0	0	0
2017	984	0	0	0	0	0
2018	1511	0	0	0	0	0
2019	1155	0	0	0	0	0
2020	1160	0	0	0	0	0
2021	1160	0	0	0	0	0
2022	1160	0	0	0	0	0

Input plots

plot_length_at_age(data = data, years = c(1931, 2022))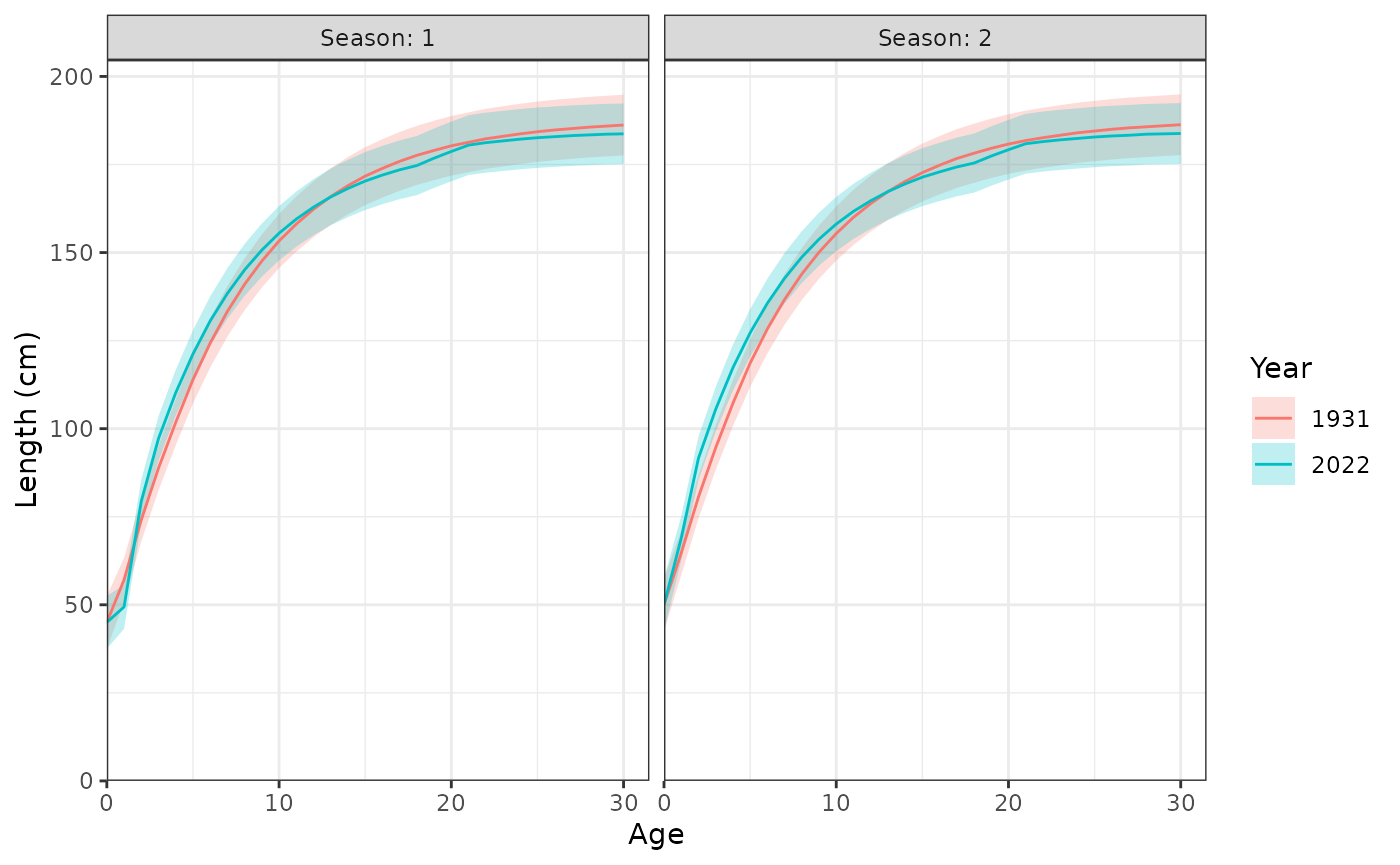

Length (cm) at age during each season.

plot_weight_at_age(data = data, years = c(1931, 2000, 2010, 2022))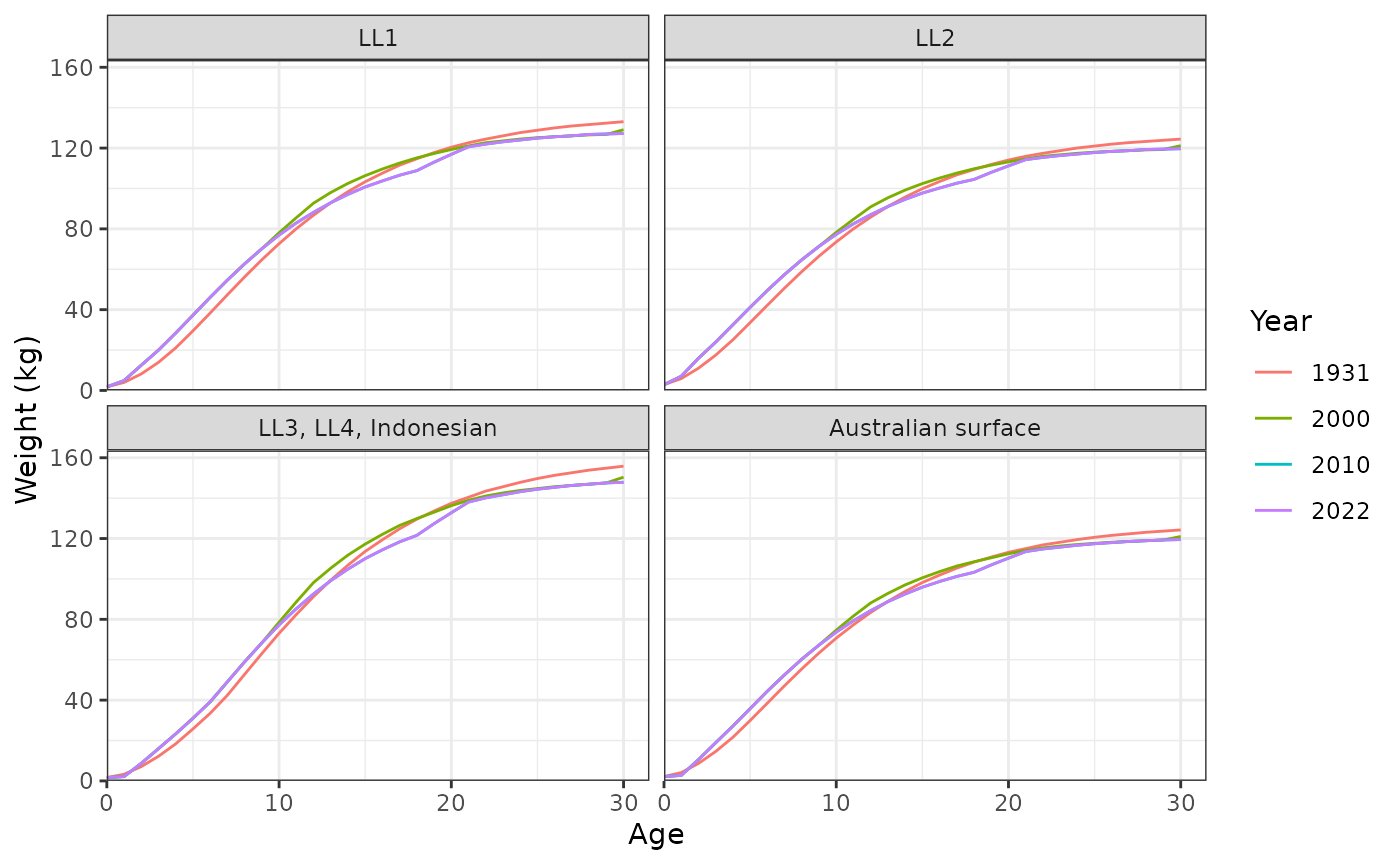

Weight (kg) at age for each fishery.

Model setup

Define the parameter list:

parameters <- get_parameters(data)
names(parameters)
#>  [1] "par_log_B0"           "par_log_psi"          "par_log_m0"          
#>  [4] "par_log_m4"           "par_log_m10"          "par_log_m30"         
#>  [7] "par_log_h"            "par_log_sigma_r"      "par_log_cpue_q"      
#> [10] "par_cpue_creep"       "par_log_cpue_sigma"   "par_log_cpue_omega"  
#> [13] "par_log_aerial_tau"   "par_log_aerial_sel"   "par_log_troll_tau"   
#> [16] "par_log_gt_q"         "par_log_hsp_q"        "par_log_tag_H_factor"
#> [19] "par_log_af_alpha"     "par_log_lf_alpha"     "par_sel_rho_y"       
#> [22] "par_sel_rho_a"        "par_log_sel_sigma"    "par_log_sel_1"       
#> [25] "par_log_sel_2"        "par_log_sel_3"        "par_log_sel_4"       
#> [28] "par_log_sel_5"        "par_log_sel_6"        "par_log_sel_7"       
#> [31] "par_rdev_y"

There is a lot of flexibility in specifying priors now:

data$priors <- get_priors(parameters)
evaluate_priors(parameters, data$priors)
#> [1] 61.79457

Use TMB’s Map option to turn parameters on/off:

map <- get_map(data, parameters)

Using the data, the parameters, the parameter map, and the model (sbt_model), the AD object is created using TMBs MakeADFun function:

obj <- MakeADFun(func = cmb(sbt_model, data), parameters = parameters, map = map)

List of parameters that are on:

unique(names(obj$par))
#>  [1] "par_log_B0"        "par_log_m4"        "par_log_m30"      
#>  [4] "par_log_cpue_q"    "par_log_troll_tau" "par_log_sel_1"    
#>  [7] "par_log_sel_2"     "par_log_sel_3"     "par_log_sel_5"    
#> [10] "par_log_sel_6"     "par_log_sel_7"     "par_rdev_y"

The objective function value:

obj$fn(obj$par)
#> [1] 24653.79

Load the default parameter bounds:

bnd <- get_bounds(obj, parameters)

Optimisation

Optimise using the nlminb function:

control <- list(eval.max = 10000, iter.max = 10000)
opt <- nlminb(start = obj$par, objective = obj$fn, gradient = obj$gr, hessian = obj$he,
              lower = bnd$lower, upper = bnd$upper, control = control)
#> Warning in nlminb(start = obj$par, objective = obj$fn, gradient = obj$gr, :
#> NA/NaN function evaluation
#> Warning in nlminb(start = obj$par, objective = obj$fn, gradient = obj$gr, :
#> NA/NaN function evaluation
#> Warning in nlminb(start = obj$par, objective = obj$fn, gradient = obj$gr, :
#> NA/NaN function evaluation
#> Warning in nlminb(start = obj$par, objective = obj$fn, gradient = obj$gr, :
#> NA/NaN function evaluation
#> Warning in nlminb(start = obj$par, objective = obj$fn, gradient = obj$gr, :
#> NA/NaN function evaluation
opt <- nlminb(start = opt$par, objective = obj$fn, gradient = obj$gr, hessian = obj$he,
              lower = bnd$lower, upper = bnd$upper, control = control)
# save(opt, file = "opt.rda")
# load("opt.rda")
# opt <- nlminb(start = opt$par, objective = obj$fn, gradient = obj$gr, hessian = obj$he,
#               lower = bnd$lower, upper = bnd$upper, control = control)

Check that all parameters are estimable:

# check_estimability(obj = obj)

Try the analytical Hessian instead:

# he <- obj$he()
# he_inv <- solve(he)
# he_ch <- chol(he)
# ev <- eigen(he)
# range(ev$values)

Calculate standard deviations of all model parameters, including non linear functions of random effects and parameters specified through the ADREPORT() macro from the user template:

Simulation

Simulation can be done for any data set in the model that is passed through the RTMB function OBS. For example, the CPUE series is set up using:

cpue_log_obs <- log(cpue_obs)
cpue_log_obs <- OBS(cpue_log_obs)
lp <- -dnorm(x = cpue_log_obs, mean = cpue_log_pred, sd = cpue_sig, log = TRUE)

This allows a call to obj$simulate()$cpue_log_obs. For example:

# obj$simulate()$cpue_log_obs
# obj$simulate()$troll_log_obs
# obj$simulate()$aerial_log_obs
# obj$simulate()$gt_nrec
# obj$simulate()$hsp_nK
# obj$simulate()$pop_nP
plot(log(data$cpue_obs), col = 2)
for (i in 1:10) lines(obj$simulate()$cpue_log_obs)

Data sets for which simulation is available include:

cpue_log_obs
troll_log_obs
aerial_log_obs
gt_nrec
hsp_nK
pop_nP

But not:

af_obs
lf_obs
cpue_lfs

Simulation is also required for calculating OSA residuals and to use the checkConsistency function. Unfortunately, the RTMB function checkConsistency does not work yet because not all data types are defined using densities that have simulation support within the model (i.e., the AFs and LFs).

# chk <- checkConsistency(obj = obj, hessian = TRUE, estimate = TRUE, n = 100, observation.name = "cpue_log_obs")
# chk
# s <- summary(chk)
# s
# s$marginal$p.value

Plot outputs

Model fits

plot_cpue(data = data, object = obj, nsim = 10)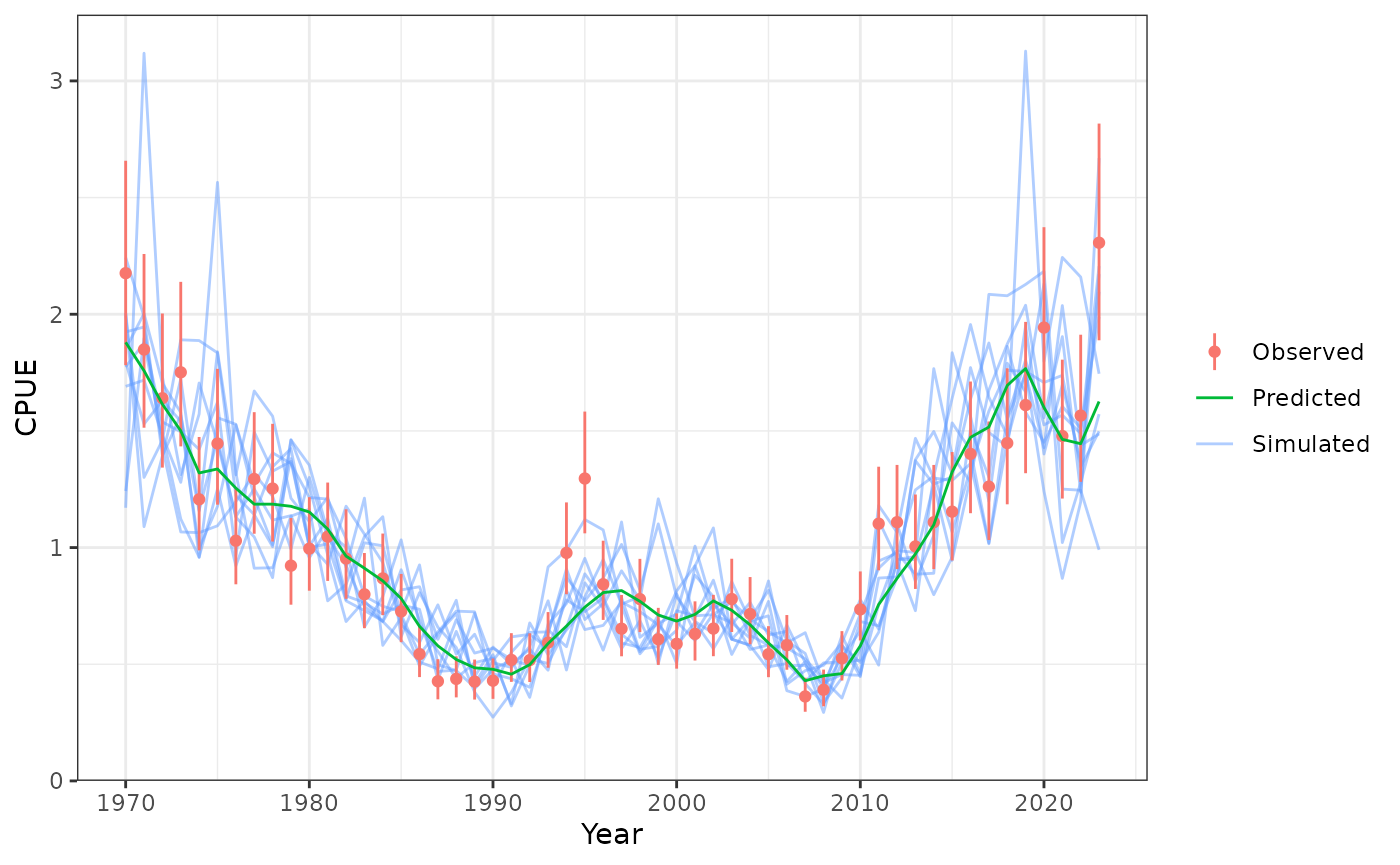

Model fits to CPUE.

plot_aerial_survey(data = data, object = obj, nsim = 10)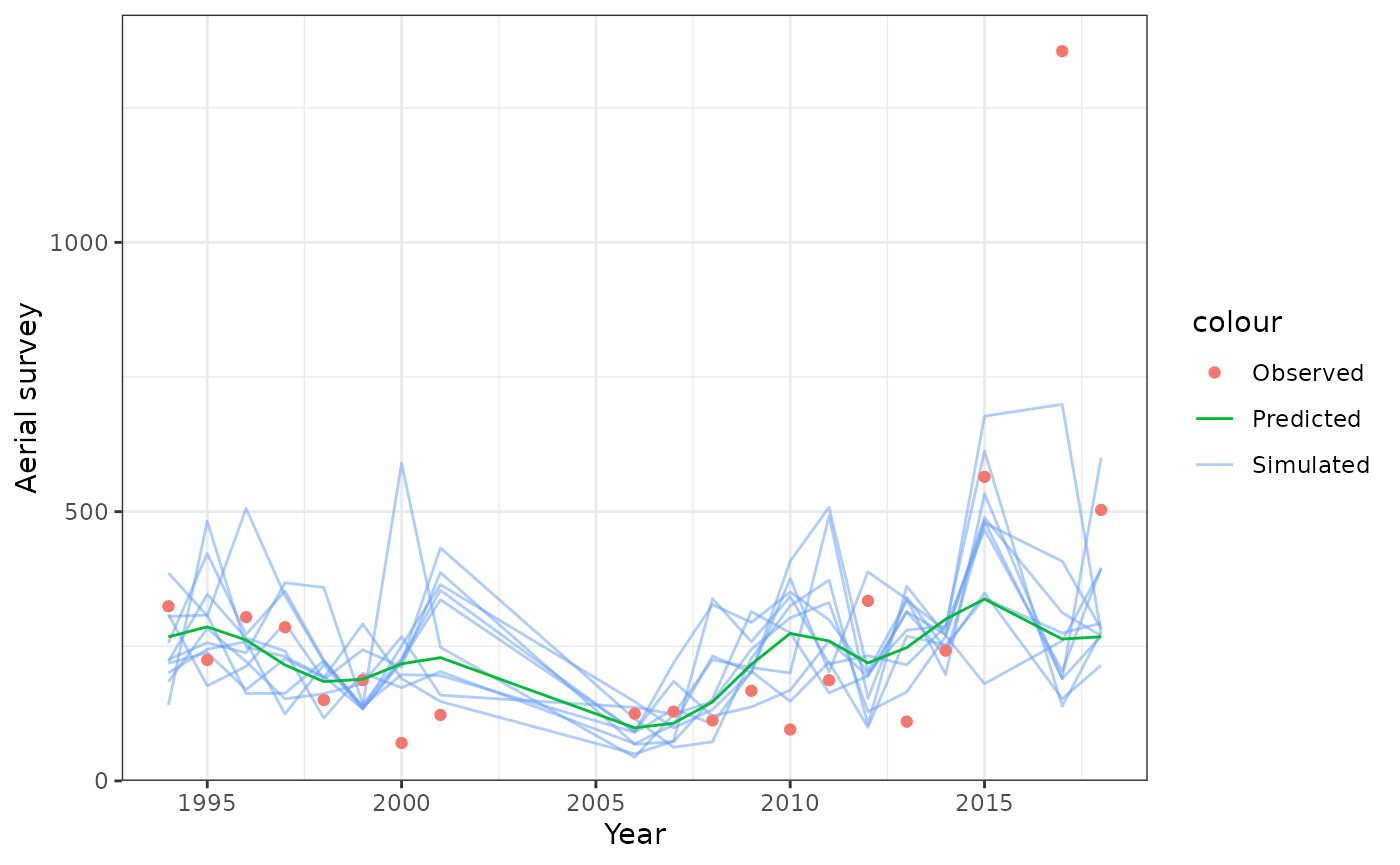

Model fits to aerial surveys.

plot_lf(data = data, object = obj, fishery = "LL1")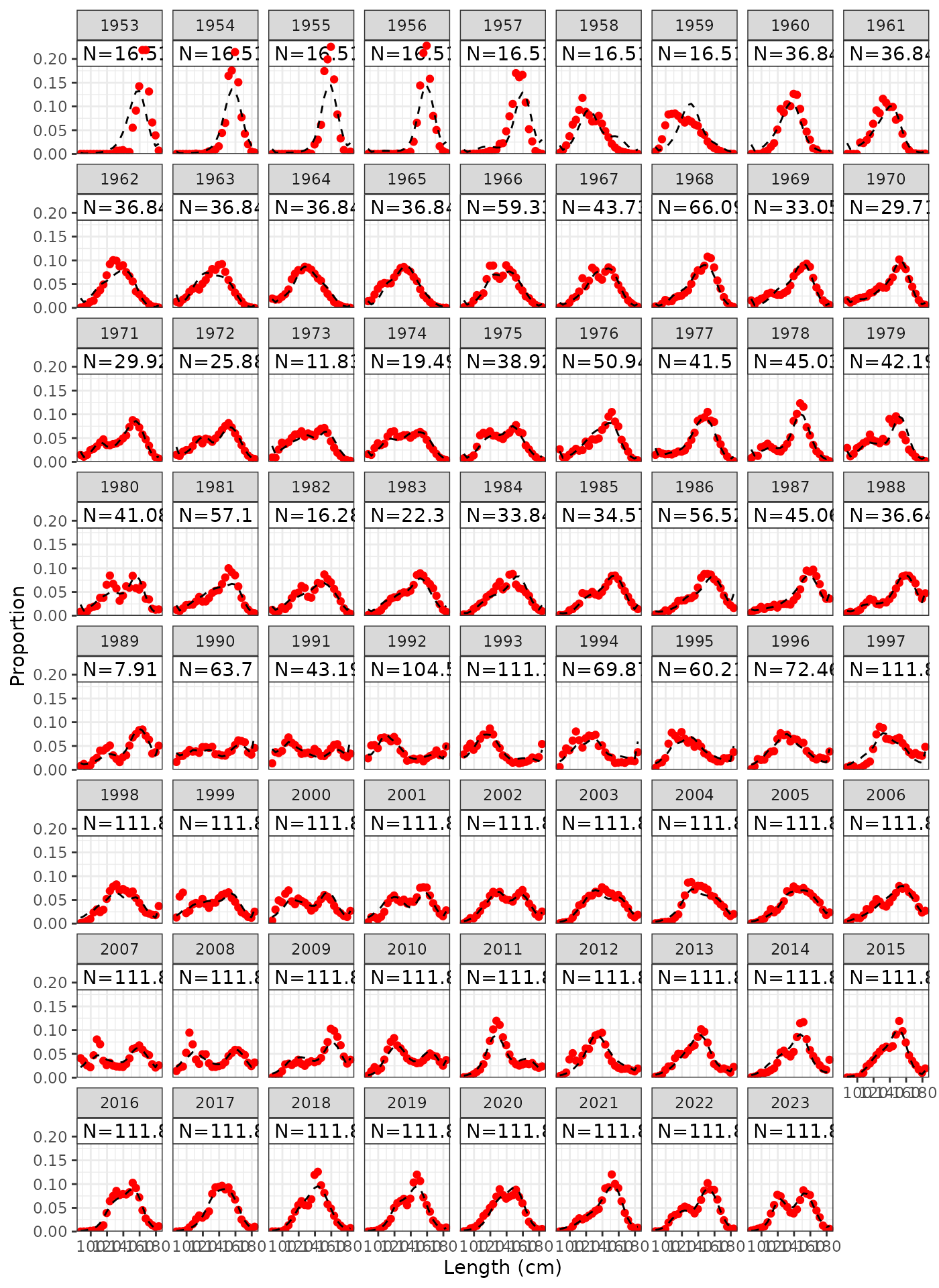

Model fits to LL1 length frequencies.

plot_lf(data = data, object = obj, fishery = "LL2")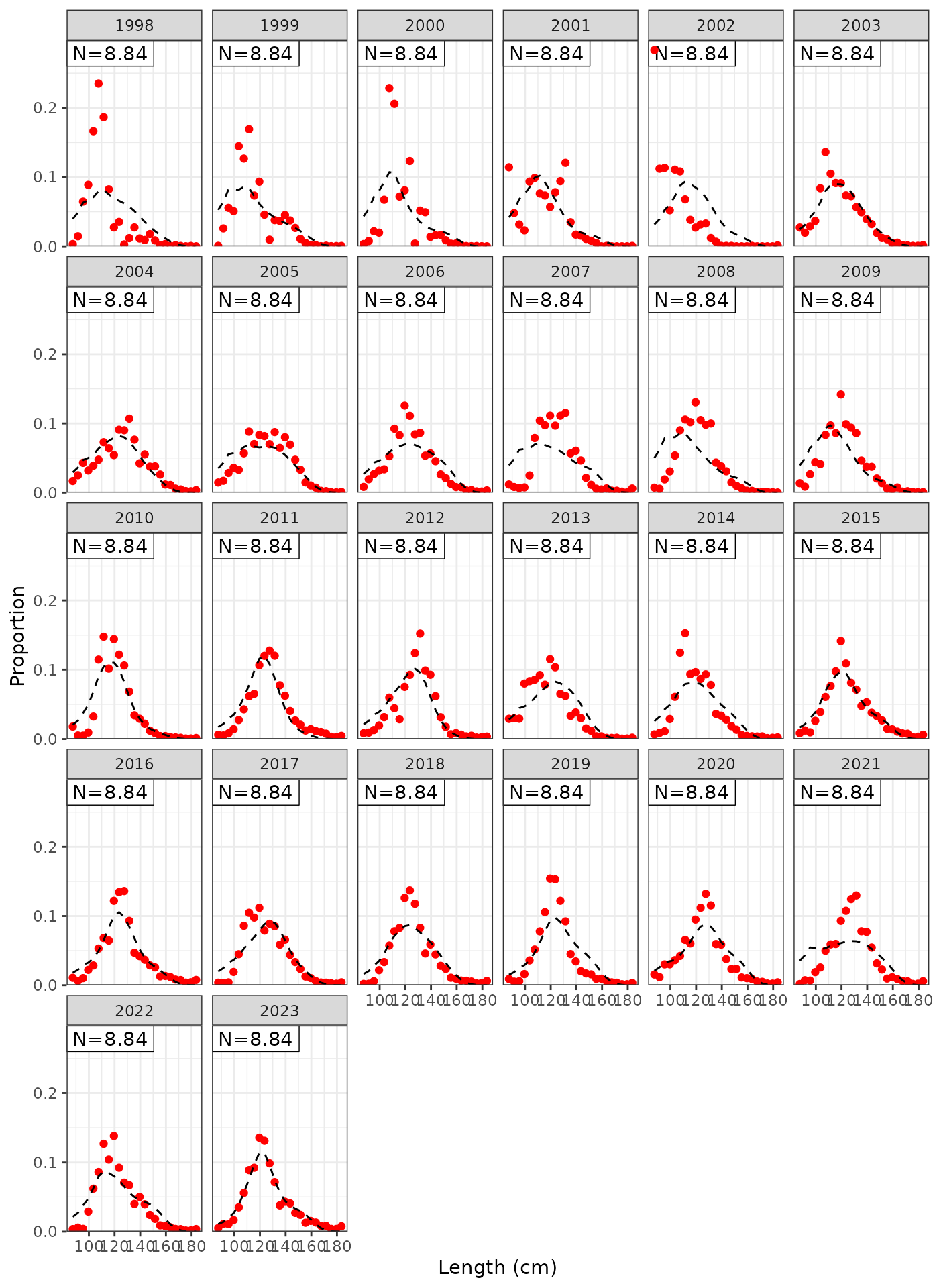

Model fits to LL2 length frequencies.

plot_lf(data = data, object = obj, fishery = "LL3")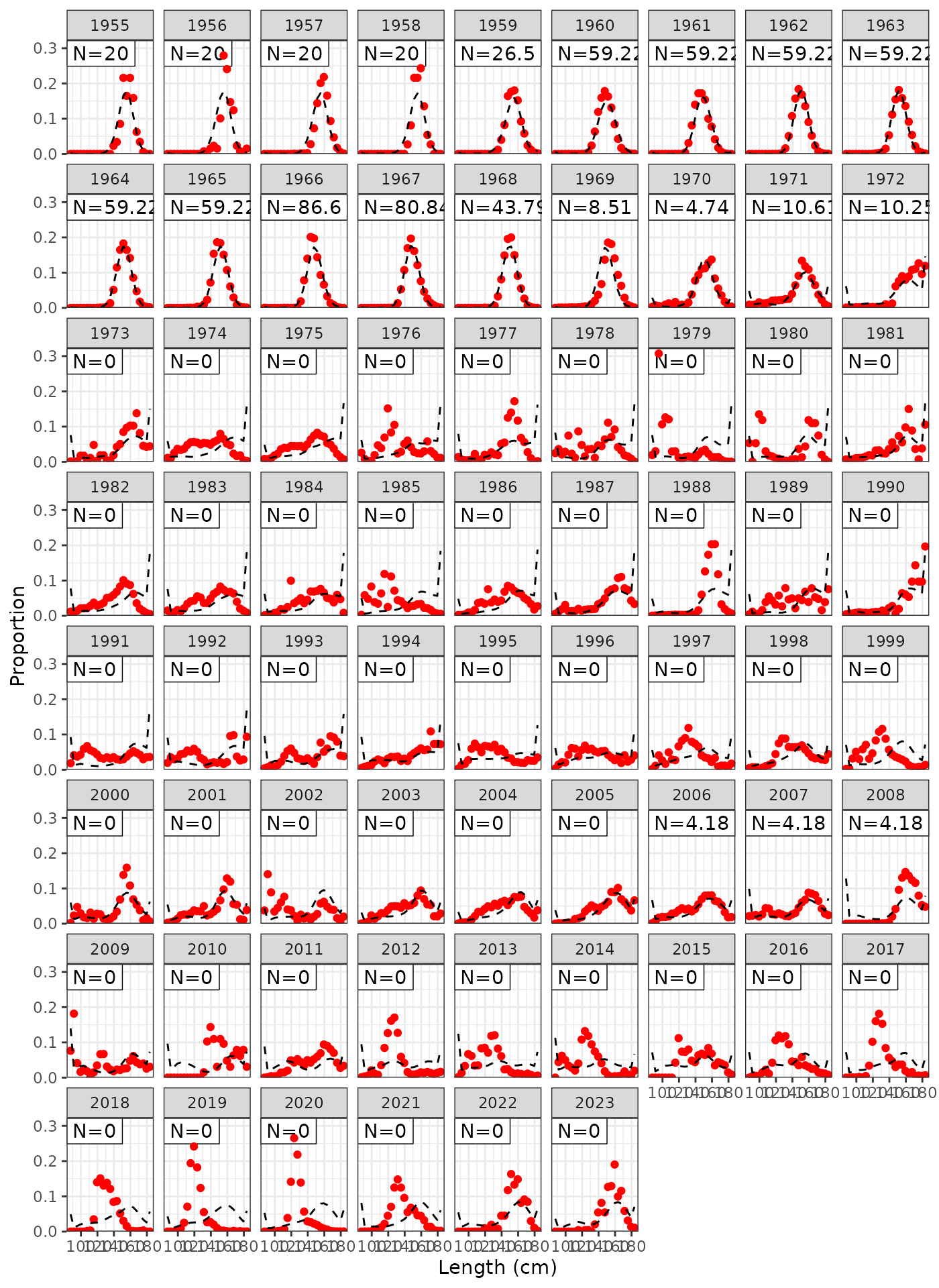

Model fits to LL3 length frequencies.

plot_lf(data = data, object = obj, fishery = "LL4")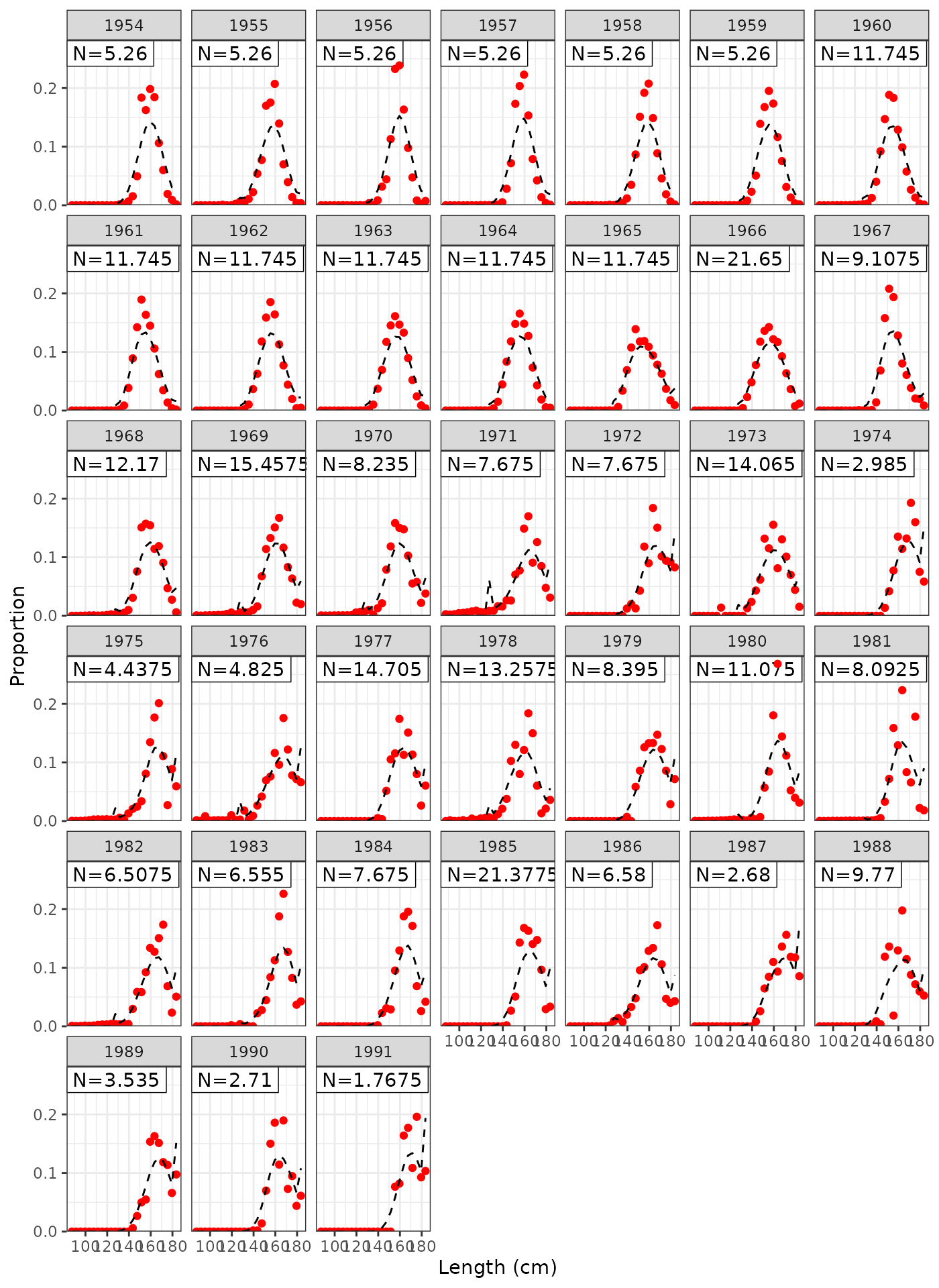

Model fits to LL4 length frequencies.

plot_af(data = data, object = obj, fishery = "Indonesian")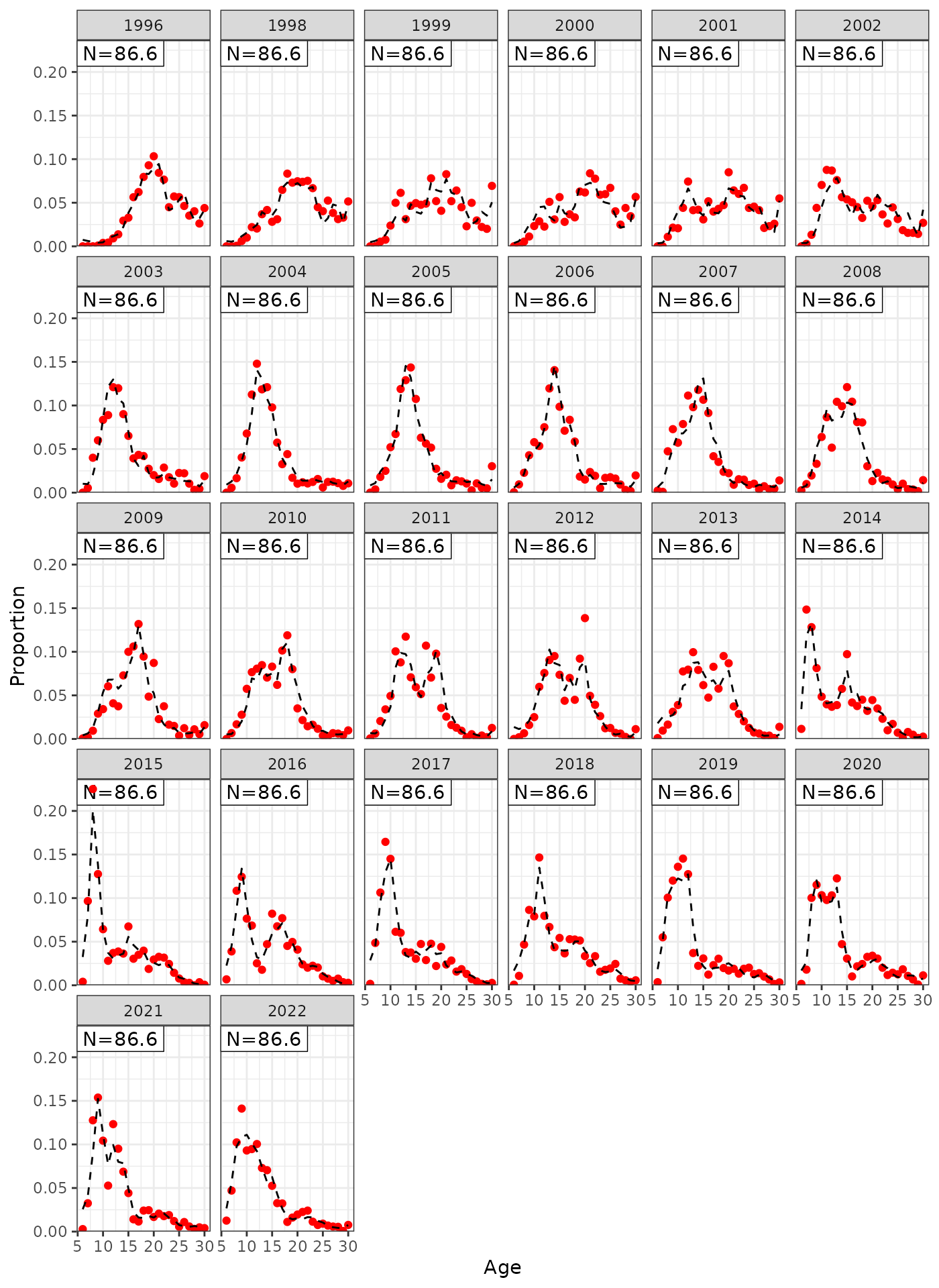

Model fits to Indonesian age compositions.

plot_af(data = data, object = obj, fishery = "Australian")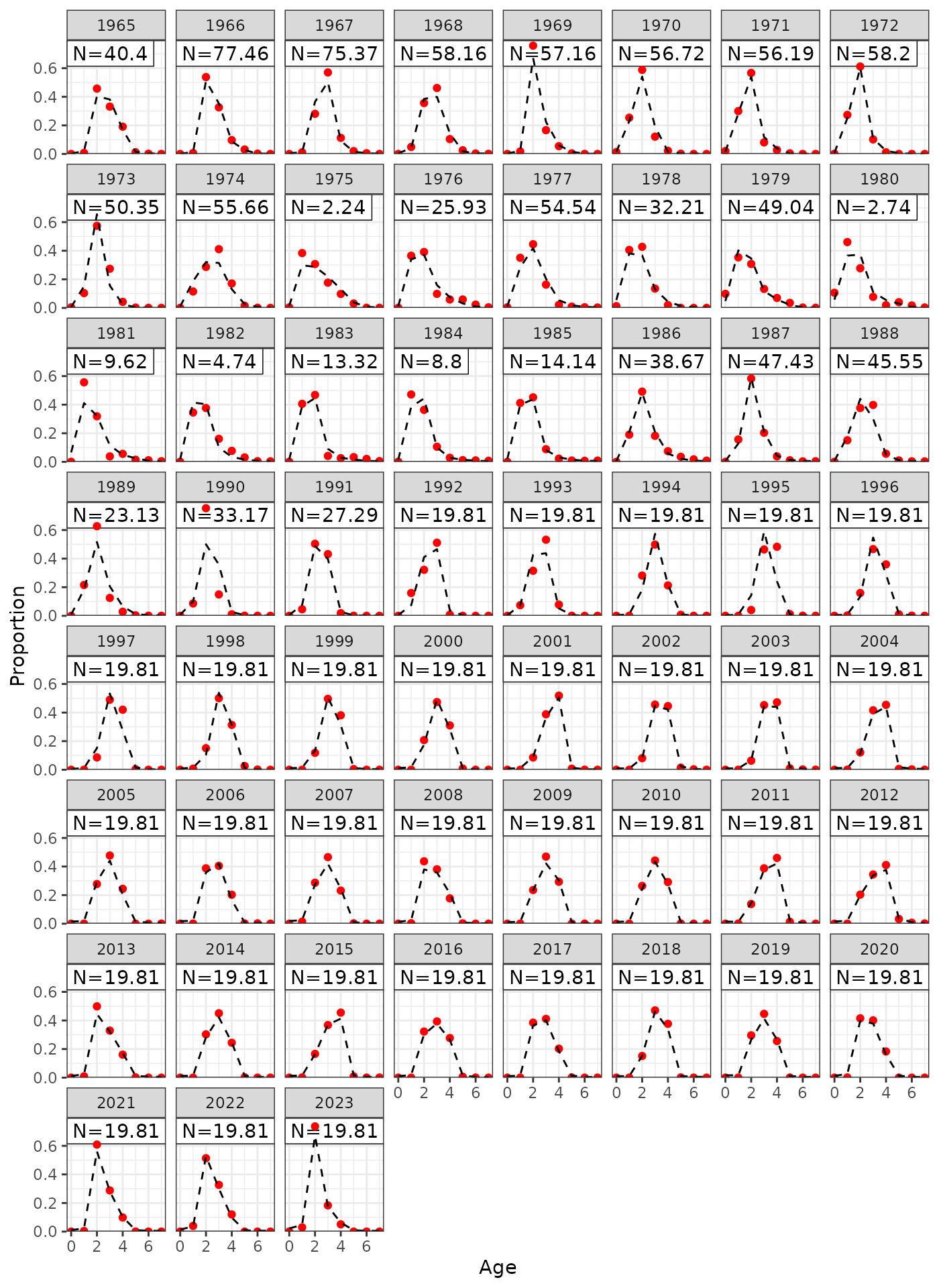

Model fits to Australian age compositions.

I think that not all of the catch is being taken for LL4 because there are years where there is catch but no LFs but we’ve set this fishery to direct removals.

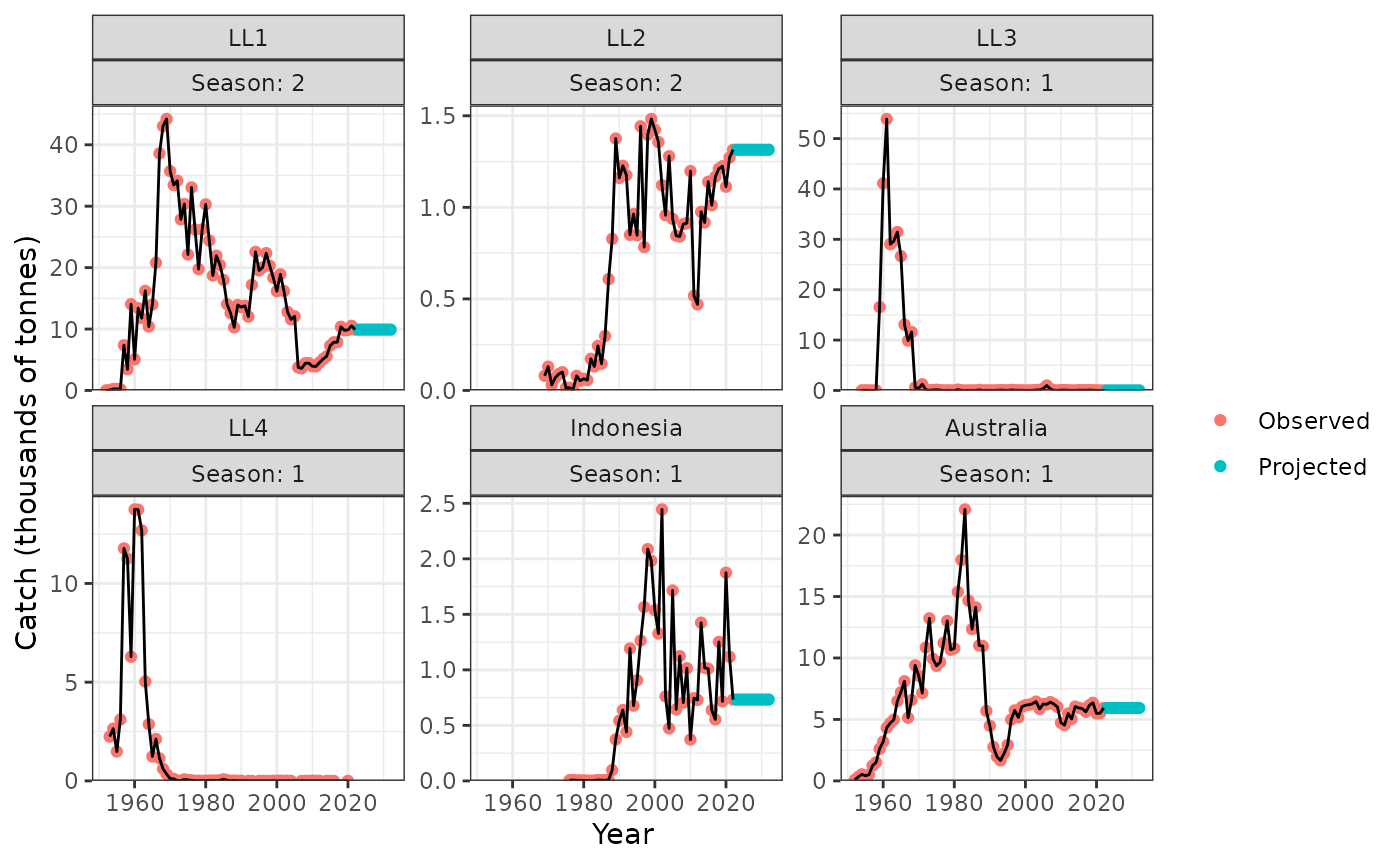
plot_catch(data = data, object = obj)
#> [1] "The maximum catch difference was: 18.98"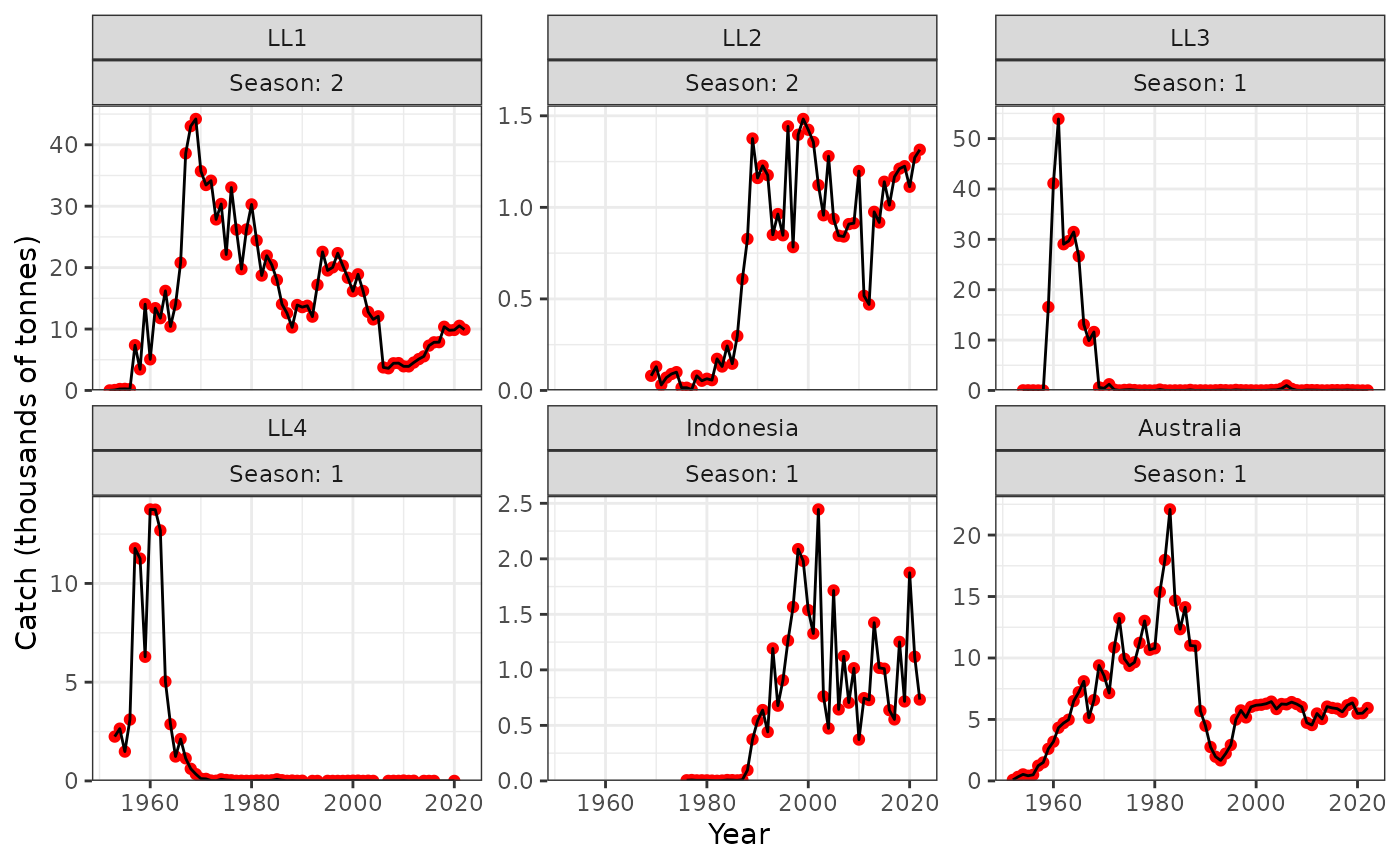

plot_catch(data = data, object = obj, plot_resid = TRUE)
#> [1] "The maximum catch difference was: 18.98"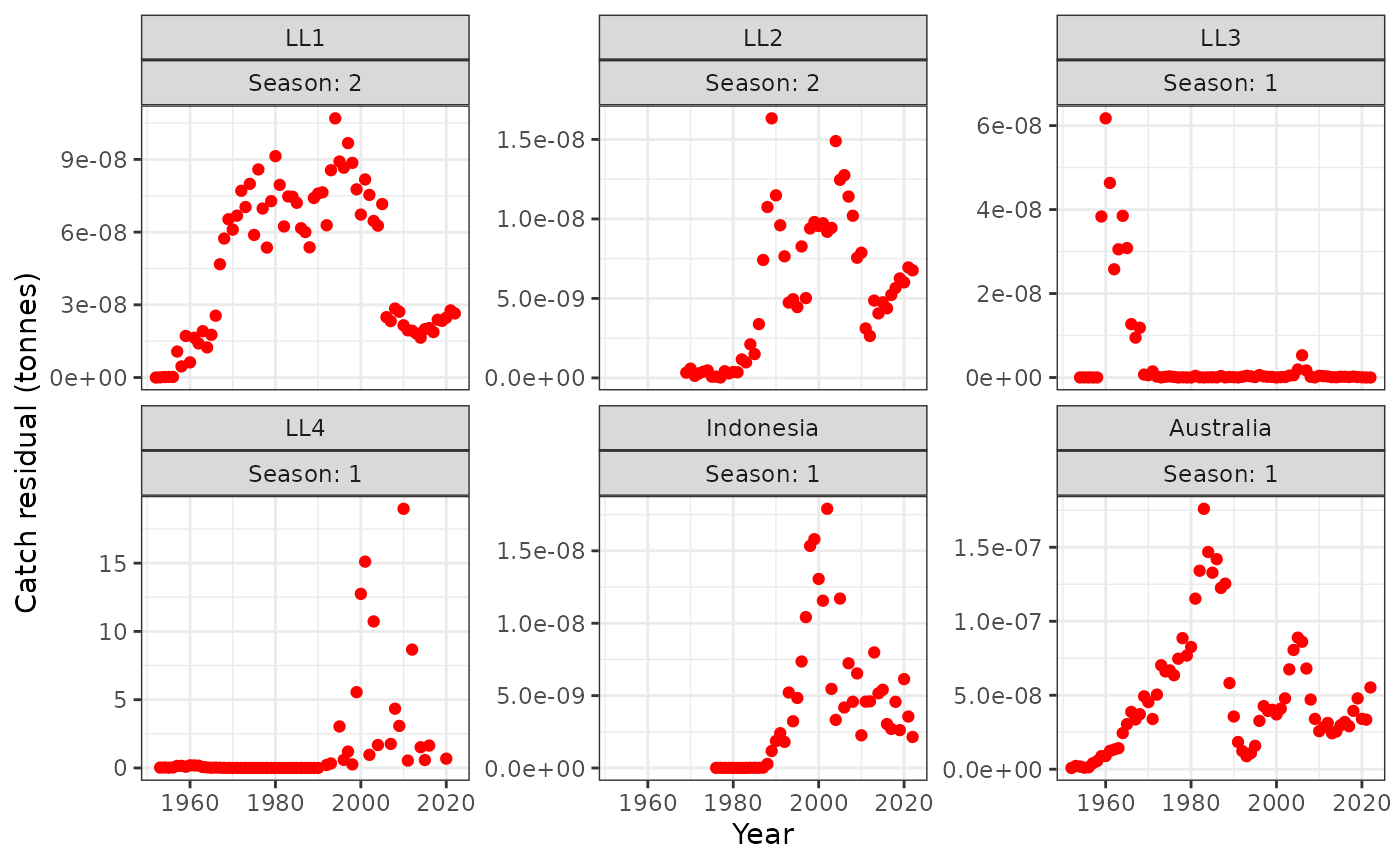

One step ahead (OSA) residuals

One step ahead (OSA) residuals are a replacement for Pearson residuals (Figure~(fig:osa1)).

osa_cpue <- oneStepPredict(obj = obj, observation.name = "cpue_log_obs", 
                           method = "oneStepGeneric", trace = FALSE)
qqnorm(osa_cpue$res); abline(0, 1)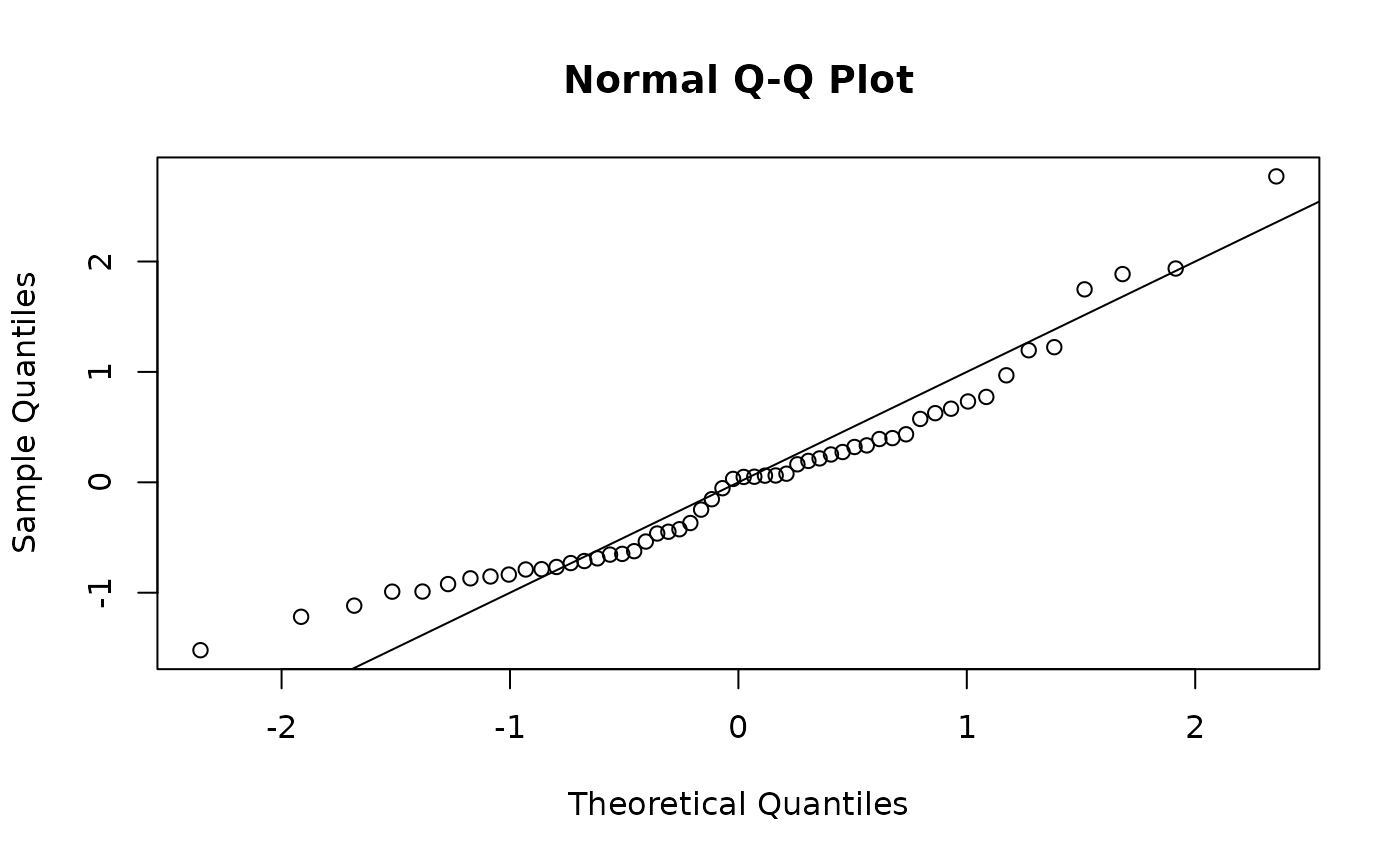

OSA residuals.

plot(osa_cpue$res); abline(-2, 0); abline(0, 0); abline(2, 0)

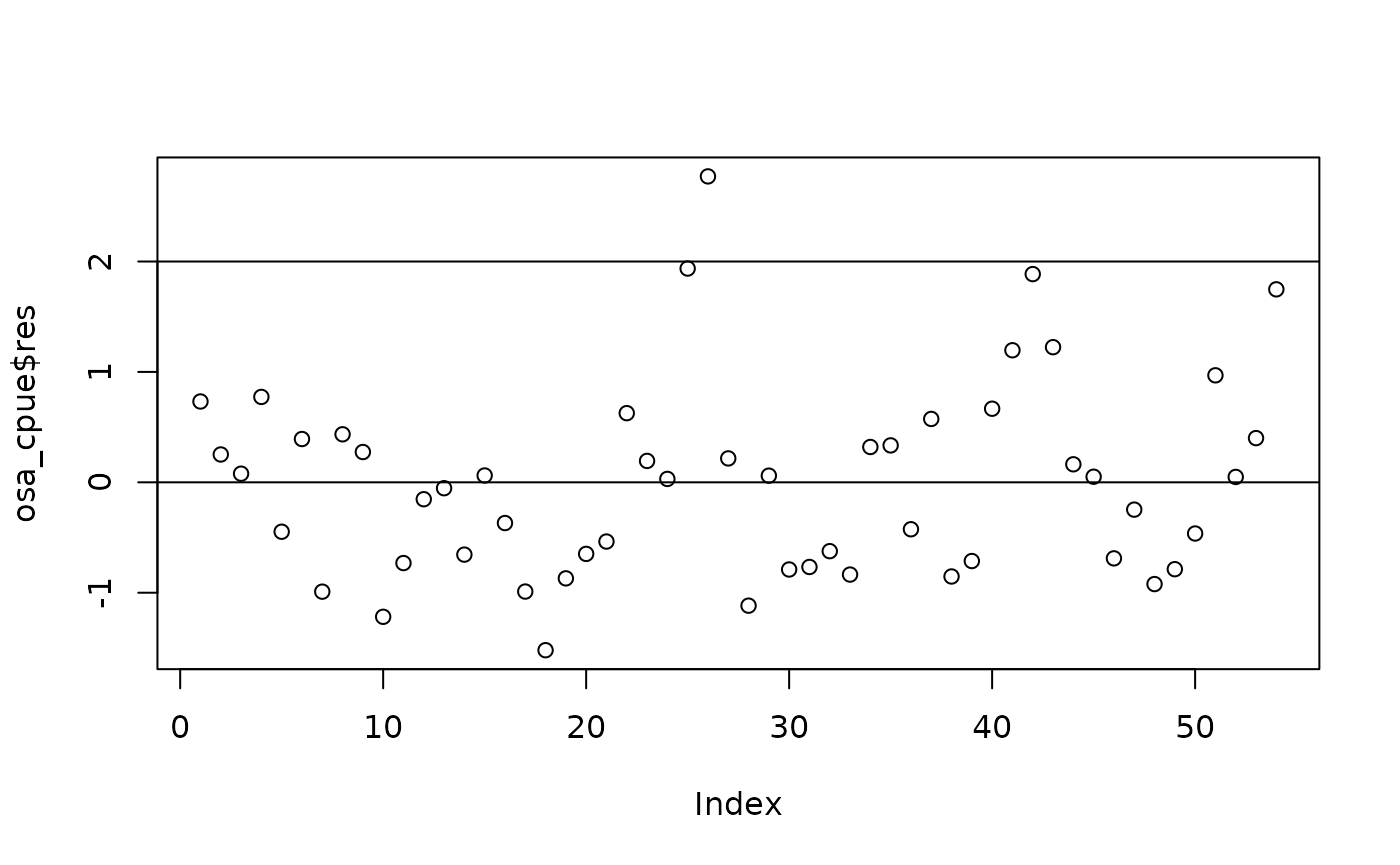
OSA residuals.

# osa <- oneStepPredict(obj = obj, method = "fullGaussian", discrete = FALSE, trace = FALSE)
# osa_troll <- oneStepPredict(obj = obj, observation.name = "troll_log_obs", method = "oneStepGeneric", trace = FALSE)
# qqnorm(osa_troll$res); abline(0, 1)
# plot(osa_troll$res); abline(0, 0)
# osa_aerial <- oneStepPredict(obj = obj, observation.name = "aerial_log_obs", method = "oneStepGeneric", trace = FALSE)
# qqnorm(osa$res); abline(0, 1)
# osa_gt <- oneStepPredict(obj = obj, observation.name = "gt_nrec", method = "oneStepGeneric", discrete = TRUE, trace = FALSE)
# qqnorm(osa_gt$res); abline(0, 1)
# plot(osa_gt$res); abline(-2, 0); abline(0, 0); abline(2, 0)
# osa_hsp <- oneStepPredict(obj = obj, observation.name = "hsp_nK", method = "oneStepGeneric", discrete = TRUE, trace = FALSE)
# qqnorm(osa_hsp$res); abline(0, 1)
# plot(osa_hsp$res); abline(0, 0)
# osa_pop <- oneStepPredict(obj = obj, observation.name = "pop_nP", method = "oneStepGeneric", discrete = TRUE, trace = FALSE)
# qqnorm(osa_pop$res); abline(0, 1)
# plot(osa_pop$res); abline(0, 0)

Derived quantities

plot_rec_devs(data = data, object = obj)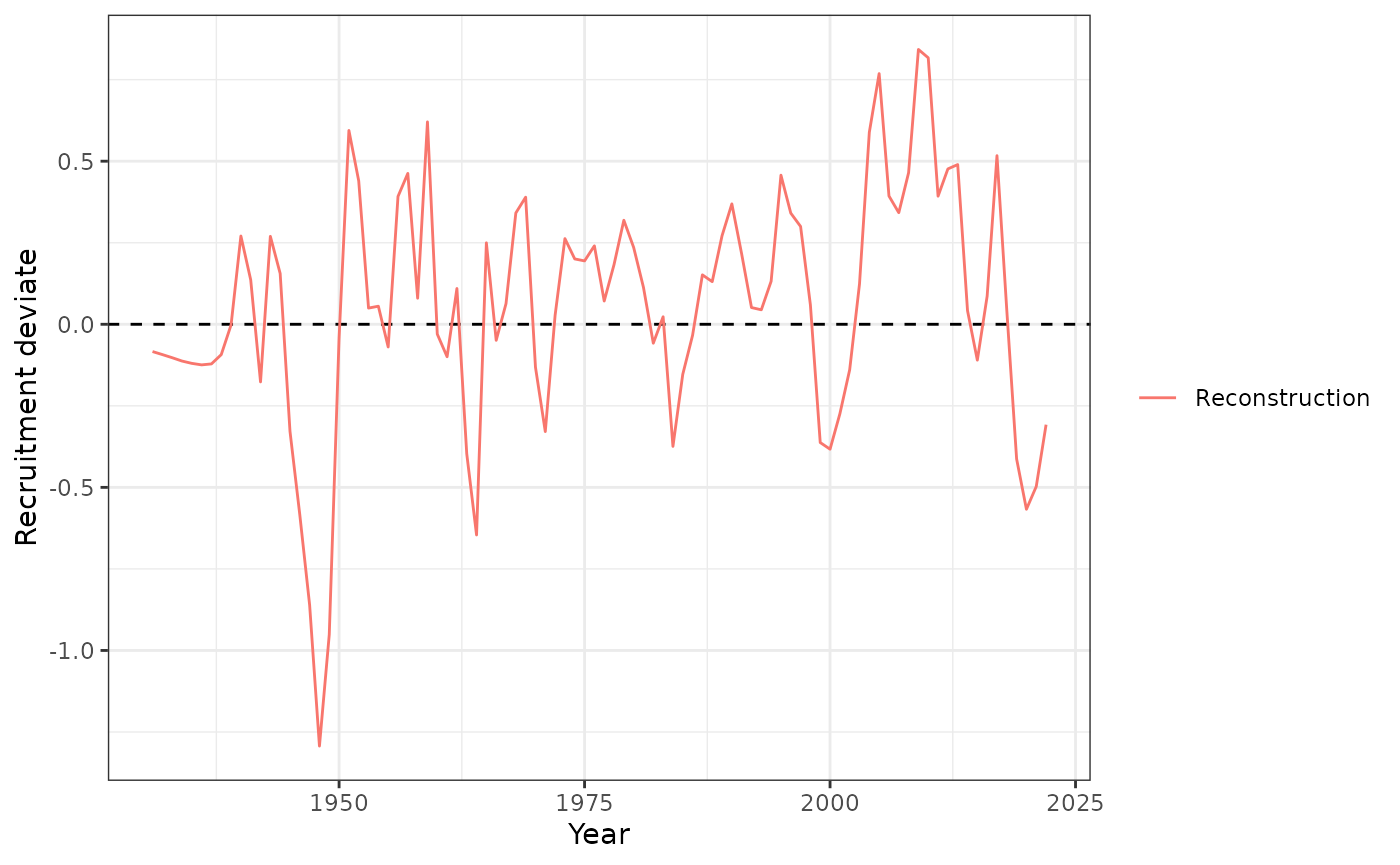

plot_recruitment(data = data, object = obj)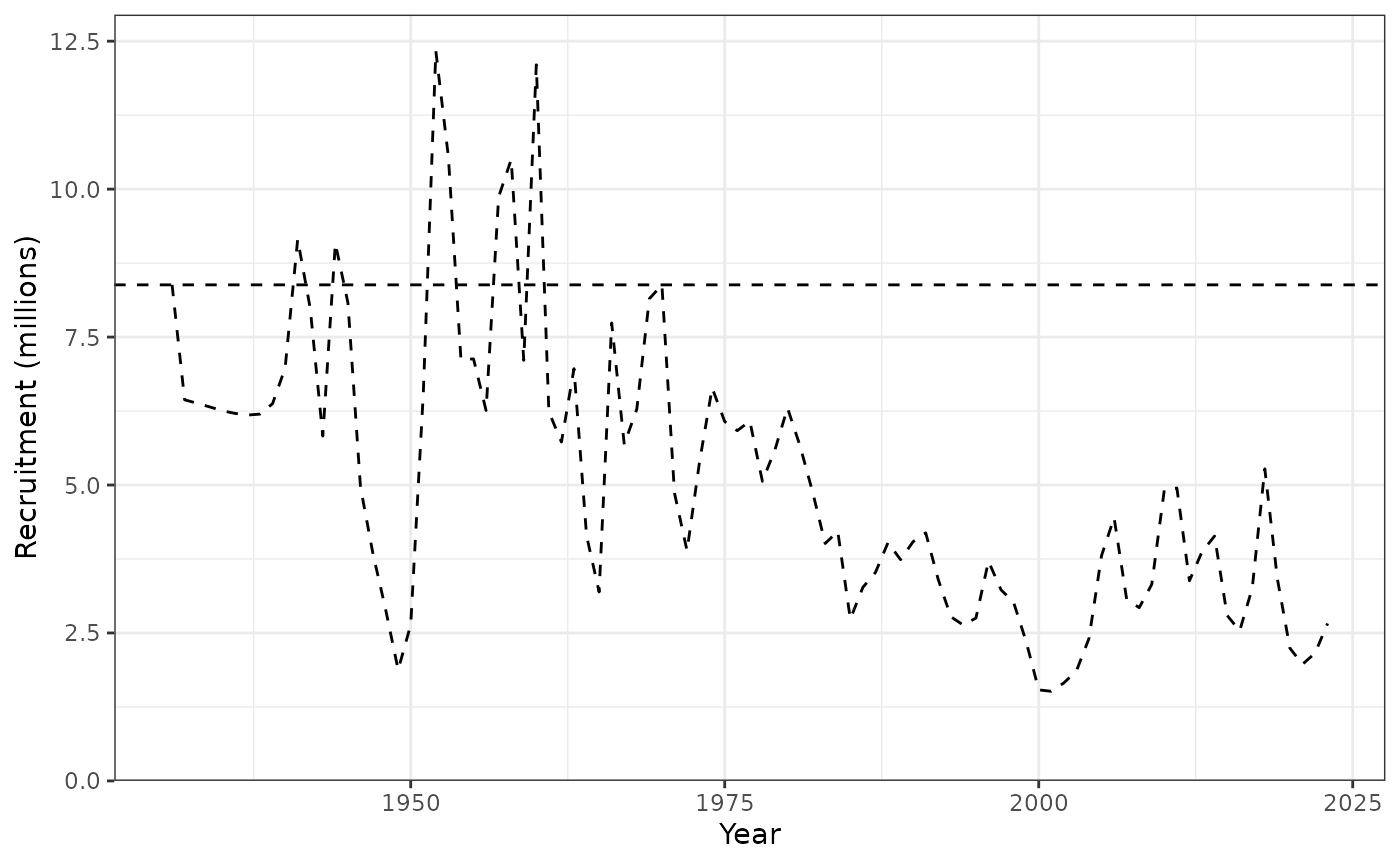

plot_natural_mortality(data = data, object = obj)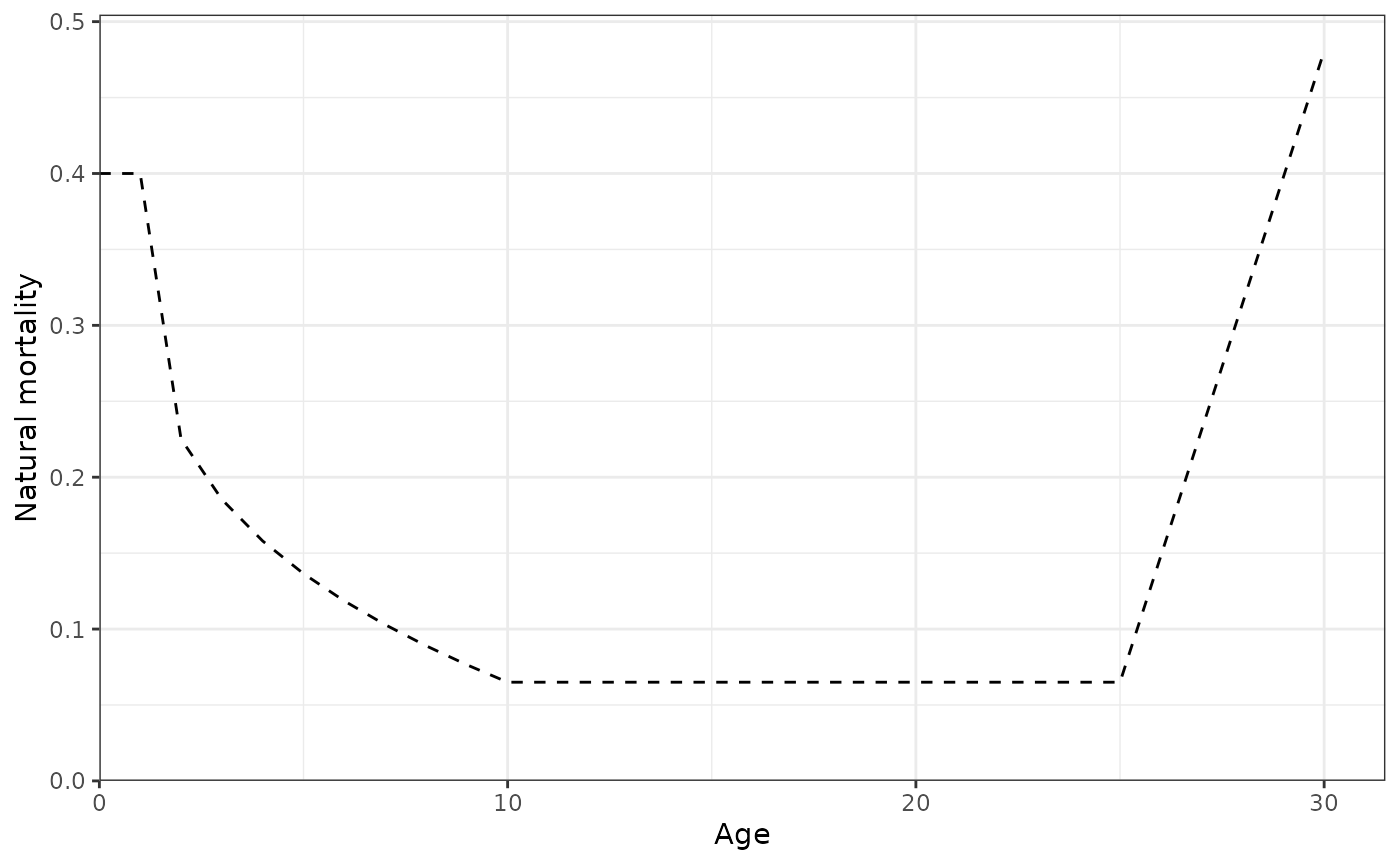

plot_initial_numbers(data = data, object = obj)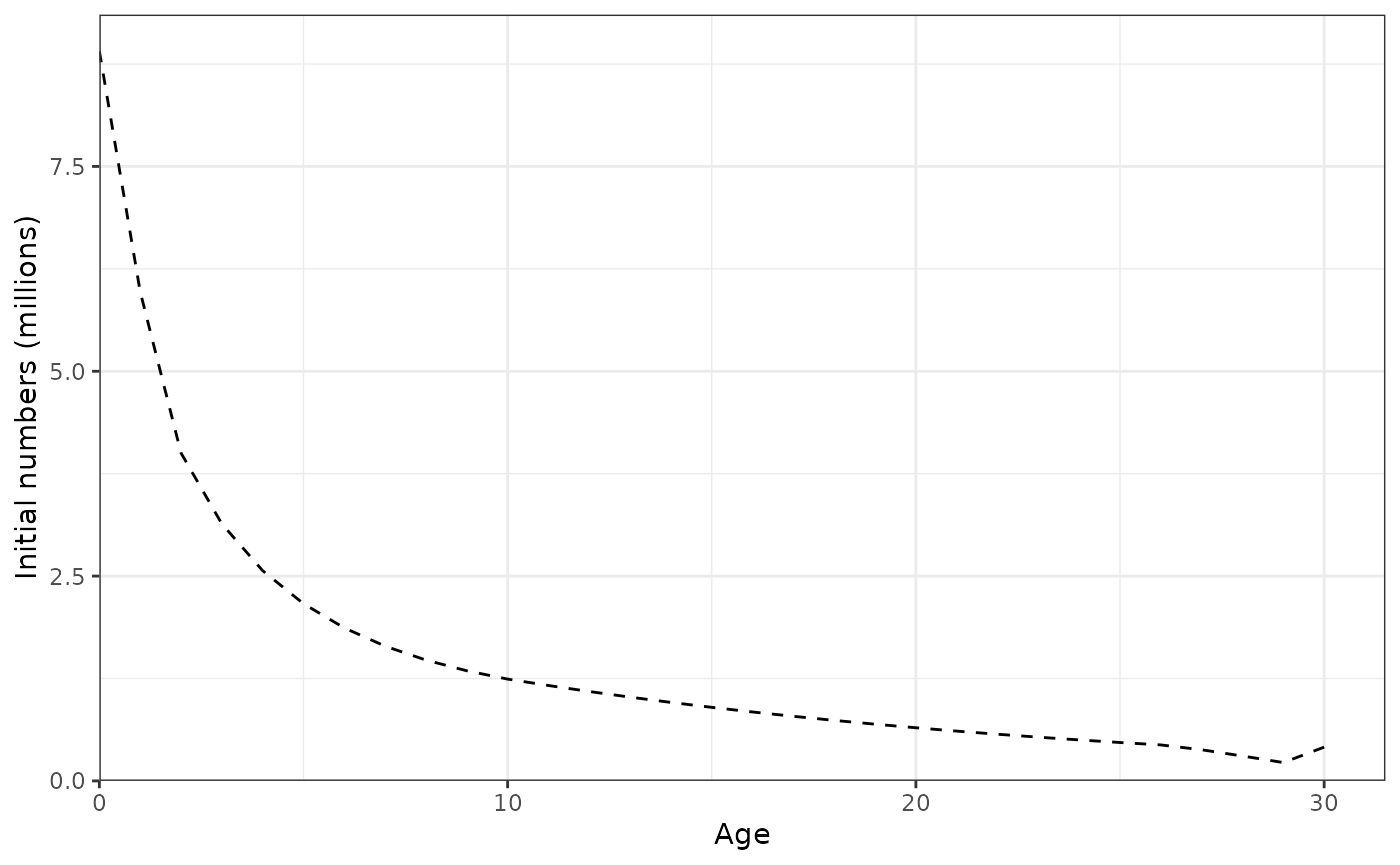

plot_hrate(data = data, object = obj, years = 1990:2010)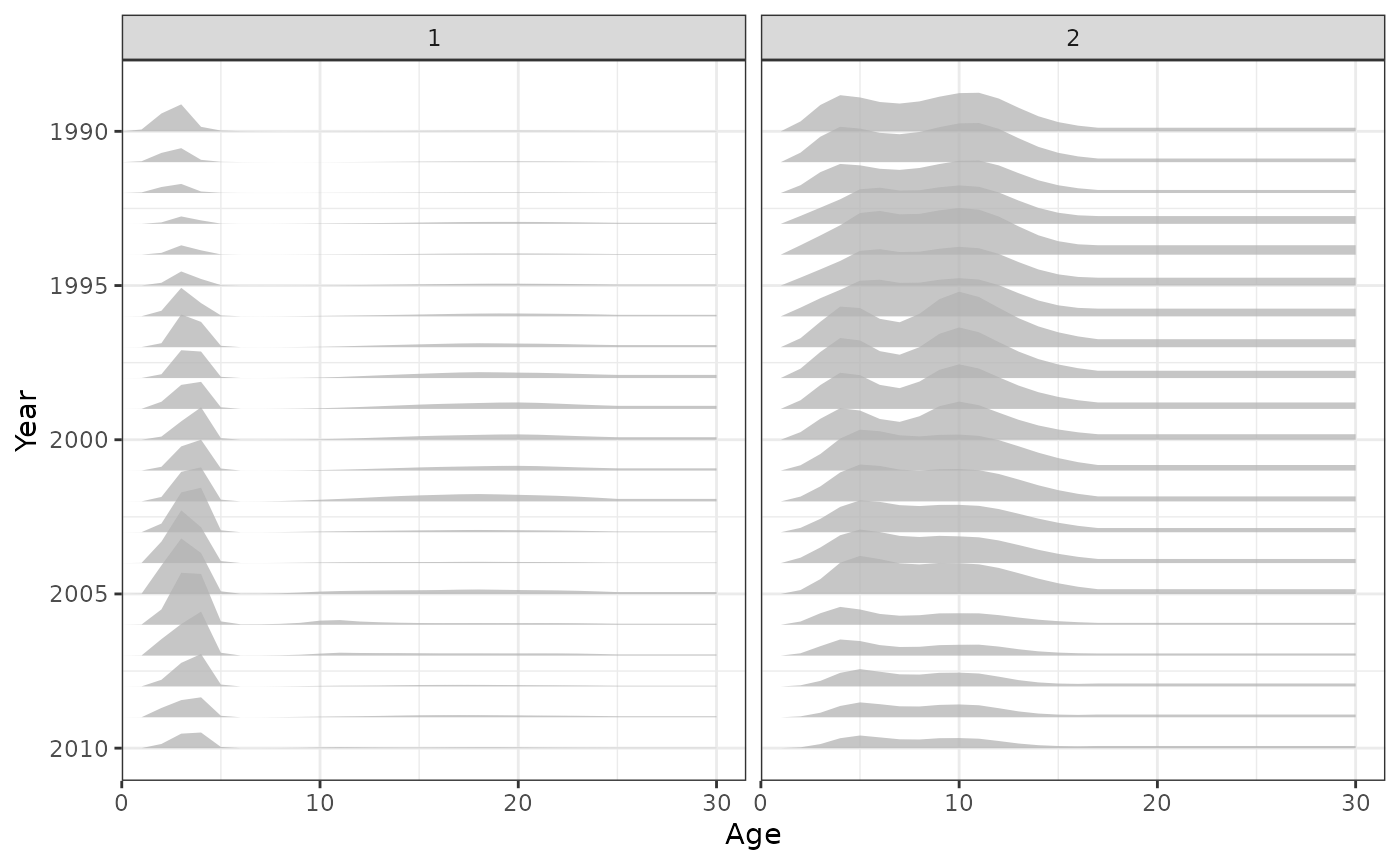

In the plots below, the different coloured blocks of years indicate blocks of parameters, vertical dashed lines indicate the minimum and maximum ages over which selectivity is estimated, and crosses to the left indicate that LF data is available during that year.

# yrs <- c(1952, 1953, 1954, seq(1955, 2020, 5), 2021, 2022)
yrs <- c(1952:2022)
plot_selectivity(data = data, object = obj, years = yrs, fisheries = "LL1")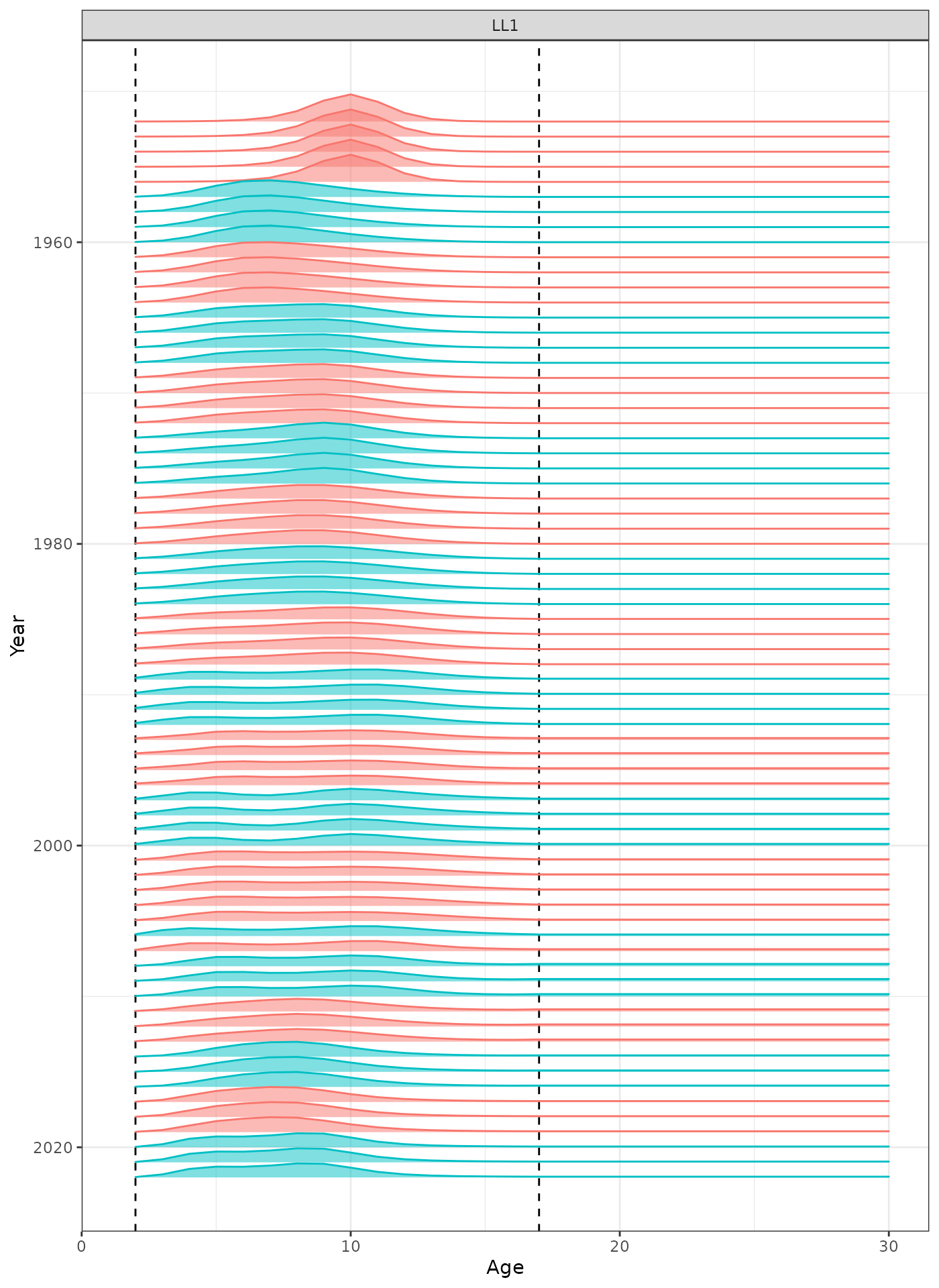

Selectivity at age by year for the LL1 fleet.

plot_selectivity(data = data, object = obj, years = yrs, fisheries = "LL2")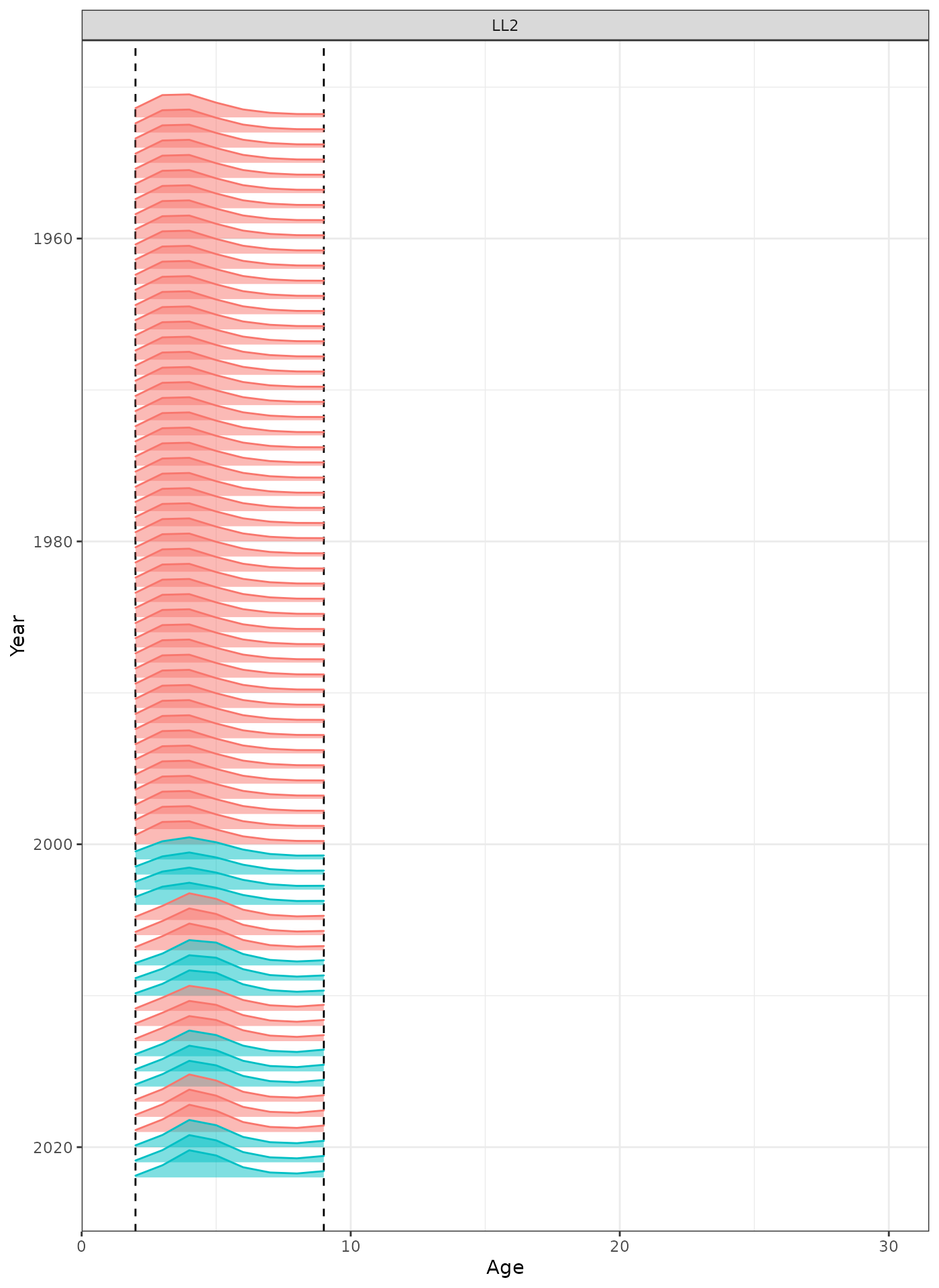

Selectivity at age by year for the LL2 fleet.

plot_selectivity(data = data, object = obj, years = yrs, fisheries = "LL3")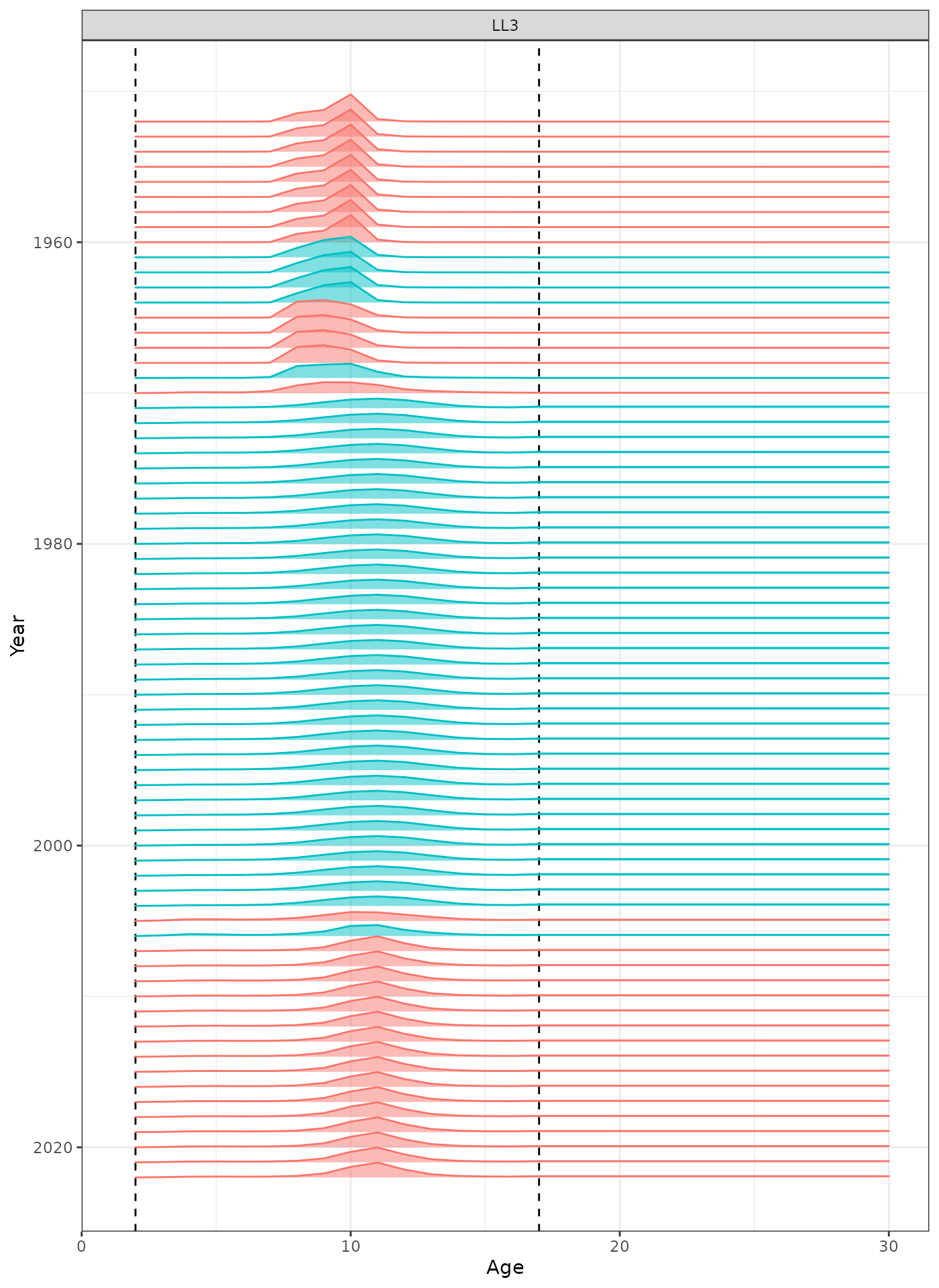

Selectivity at age by year for the LL3 fleet.

# plot_selectivity(data = data, object = obj, years = yrs, fisheries = "LL4")

plot_selectivity(data = data, object = obj, years = yrs, fisheries = "Indonesian")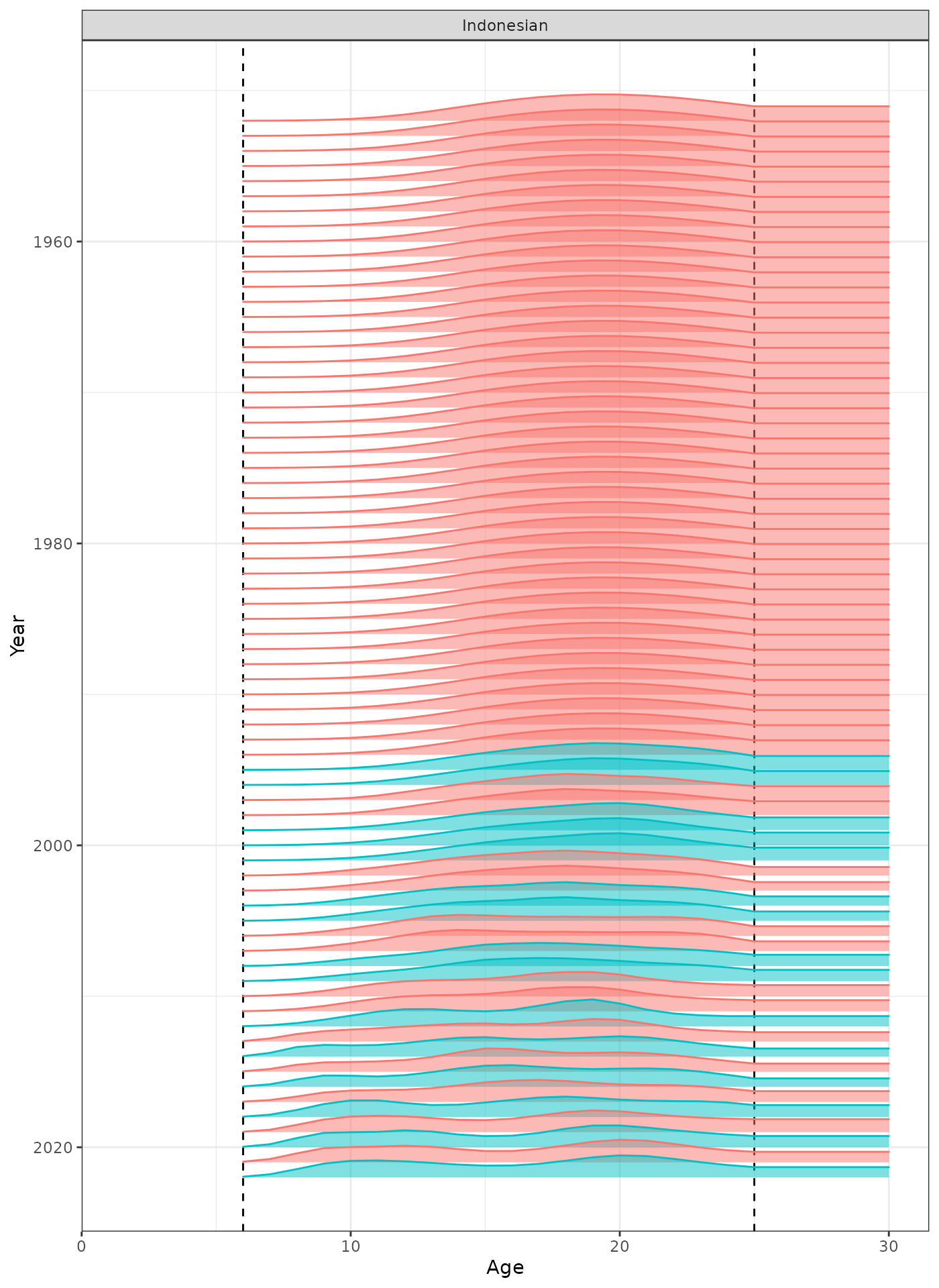

Selectivity at age by year for the Indonesian fleet.

plot_selectivity(data = data, object = obj, years = yrs, fisheries = "Australian")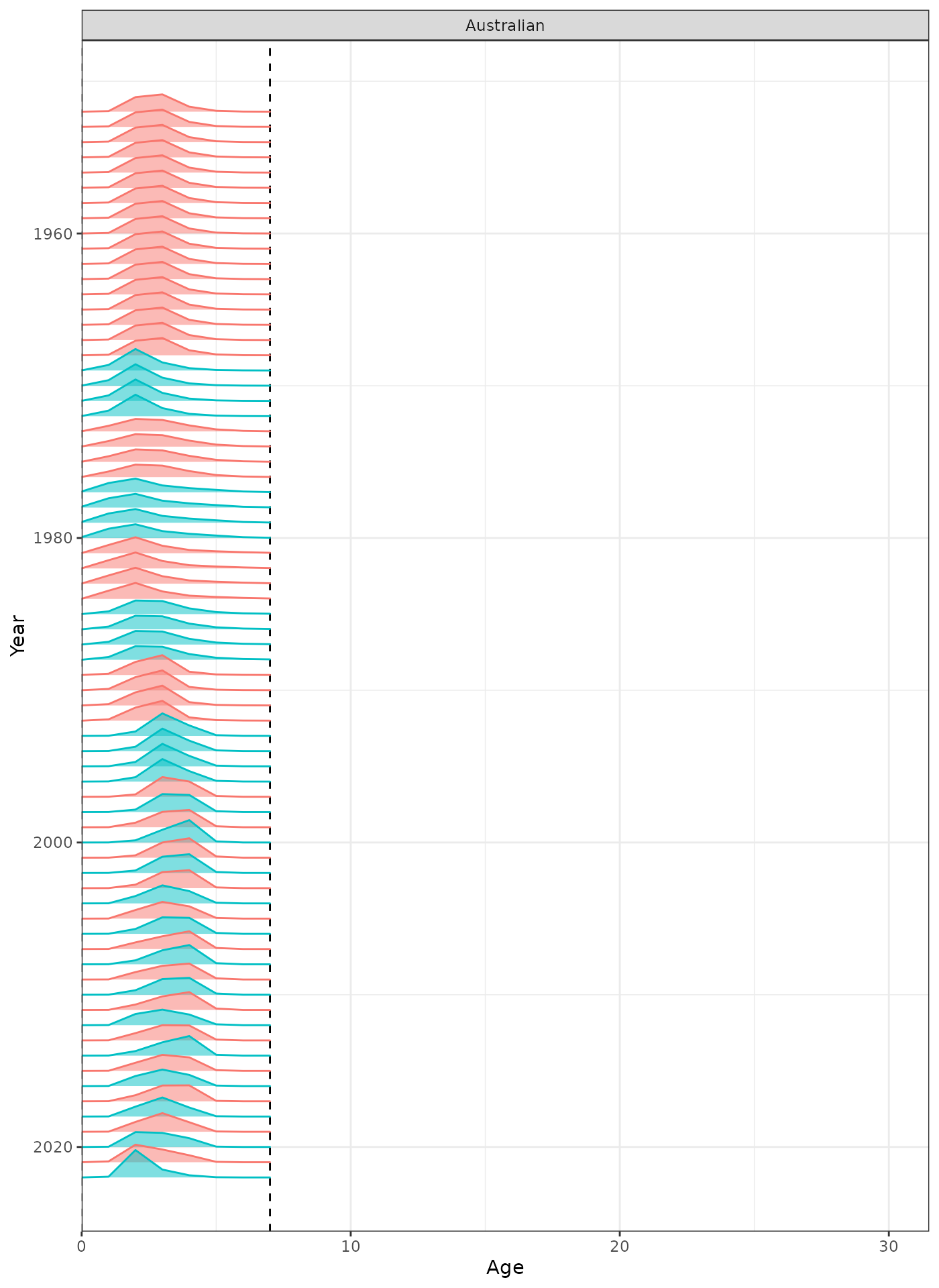

Selectivity at age by year for the Australian fleet.

plot_selectivity(data = data, object = obj, years = yrs, fisheries = "CPUE")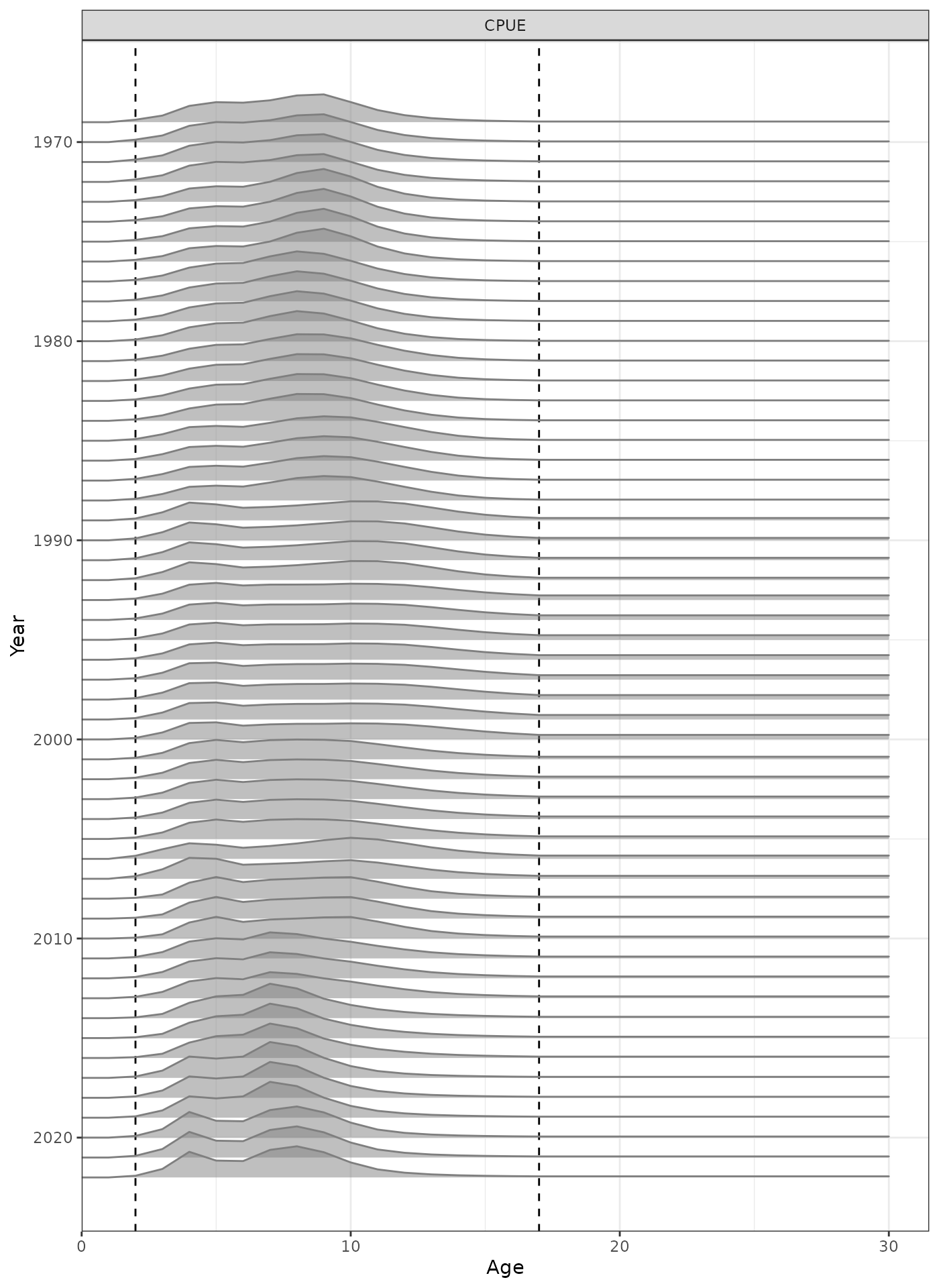

Selectivity at age by year for the CPUE index.

plot_biomass_spawning(data = data, object = obj)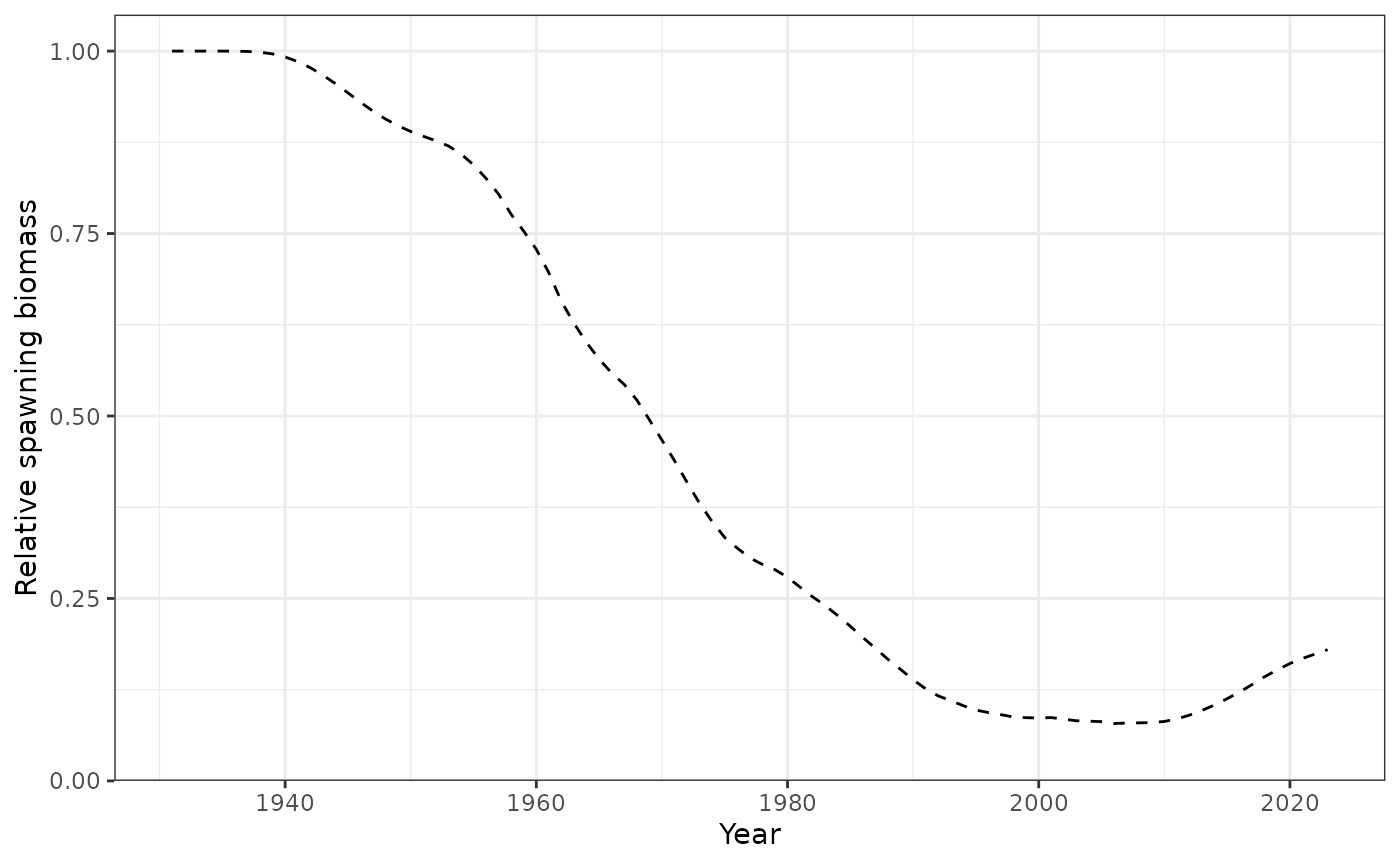

Spawning biomass by year.

Likelihood profiles

Likelihood profiles can be done for any model parameter using the function sbtprofile. The ytol argument defines the range of likelihood values to explore. A profile can be run using either using name or lincomb arguments, where the latter can be used if there are multiple parameters with the same name (e.g., par_log_sel_1).

# ytol <- 9
# prof_B0 <- sbtprofile(obj = obj, name = "par_log_B0", ytol = ytol)
# prof_m4 <- sbtprofile(obj = obj, name = "par_log_m4", ytol = ytol)
# prof_m30 <- sbtprofile(obj = obj, name = "par_log_m30", ytol = ytol)
# lincomb <- numeric(length(obj$par)); lincomb[6] <- 1
# prof_sel1 <- sbtprofile(obj = obj, lincomb = lincomb, ytol = ytol)
# save(prof_B0, prof_m4, prof_m30, prof_sel1, file = "profiles.rda")
load("profiles.rda")

Note that the profile for B0 did not work very well, likelihood for LFs was zero when B0 was too low. Need to look into this.

head(prof_B0)
obj$env$last.par.best[names(obj$par) == "par_log_B0"]
plot_profile(x = prof_B0 %>% filter(is.finite(value)), xlab = "B0")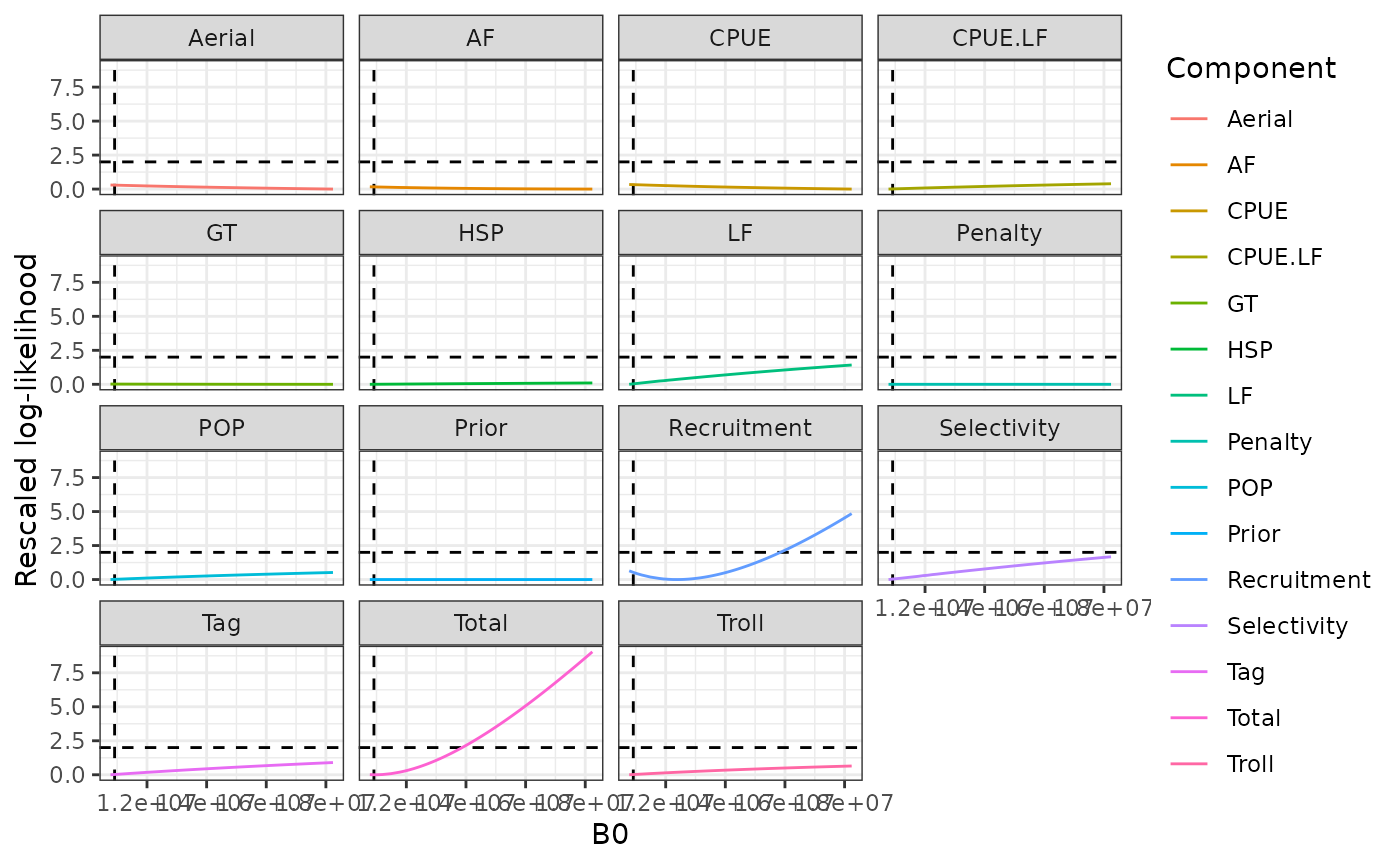

Likelihood profile for B0.

plot_profile(x = prof_m4, xlab = "M4")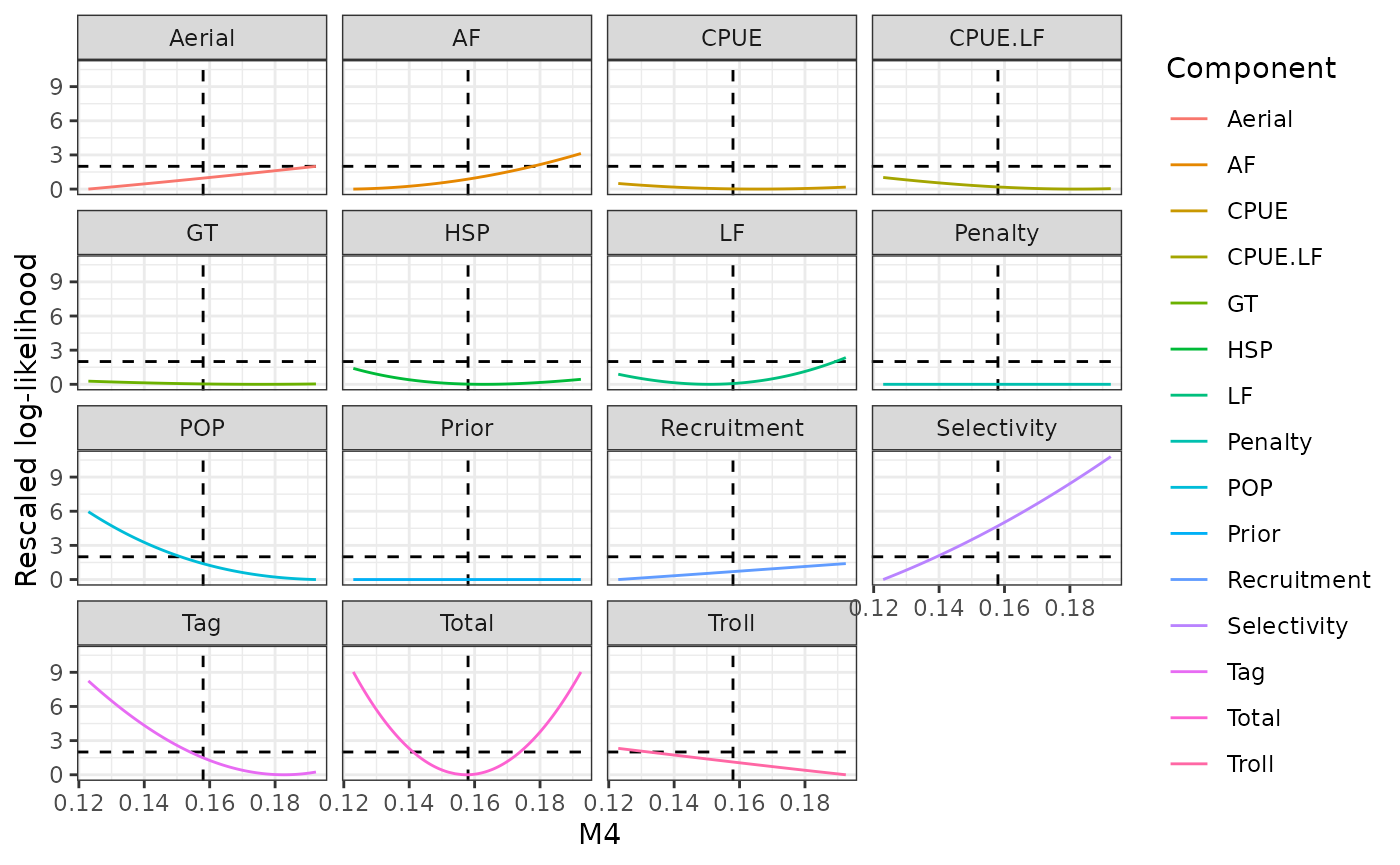

Likelihood profile for M4.

plot_profile(x = prof_m30, xlab = "M30")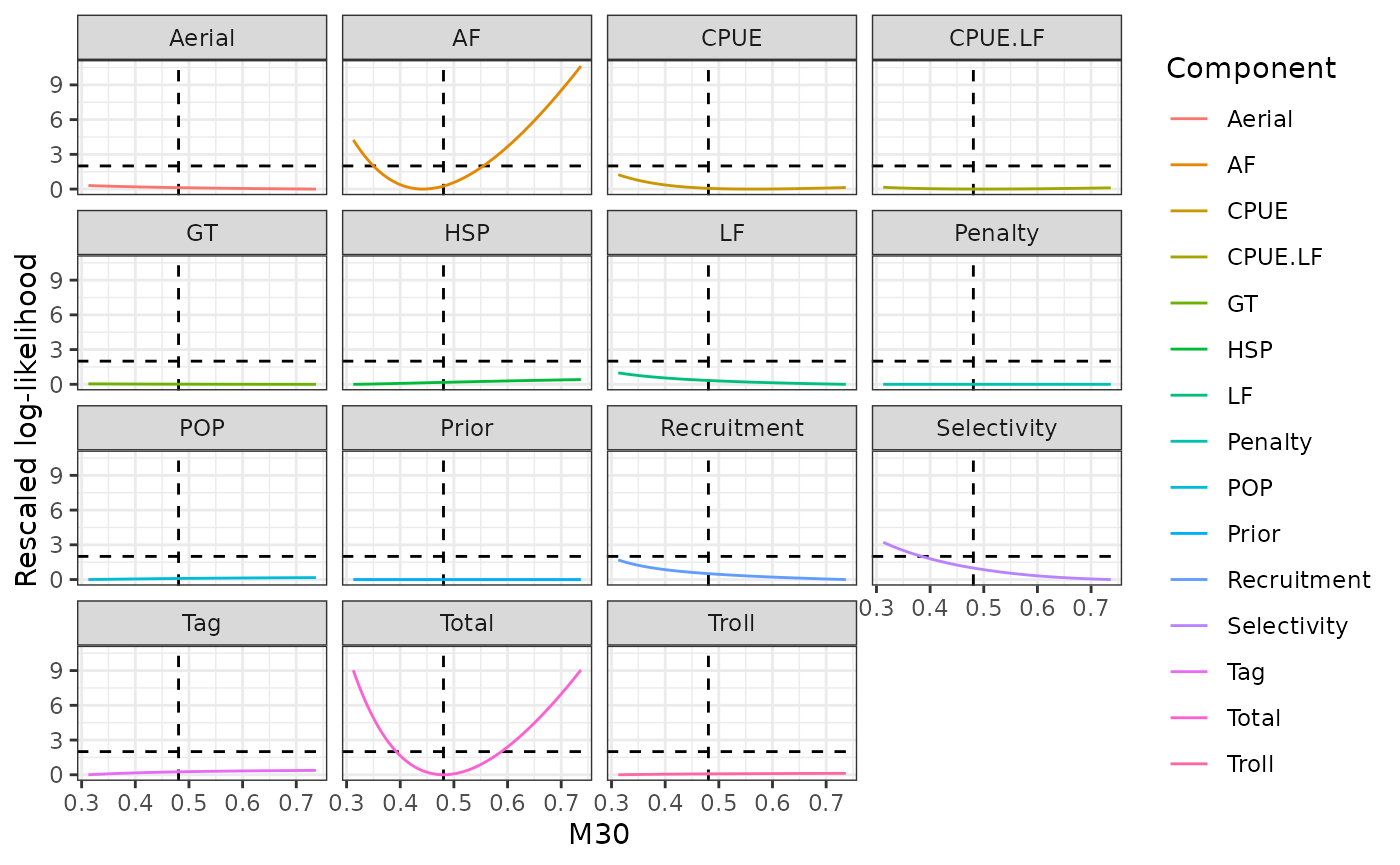

Likelihood profile for M30.

plot_profile(x = prof_sel1, xlab = "Sel1")
#> Warning: Removed 15 rows containing missing values or values outside the scale range
#> (`geom_vline()`).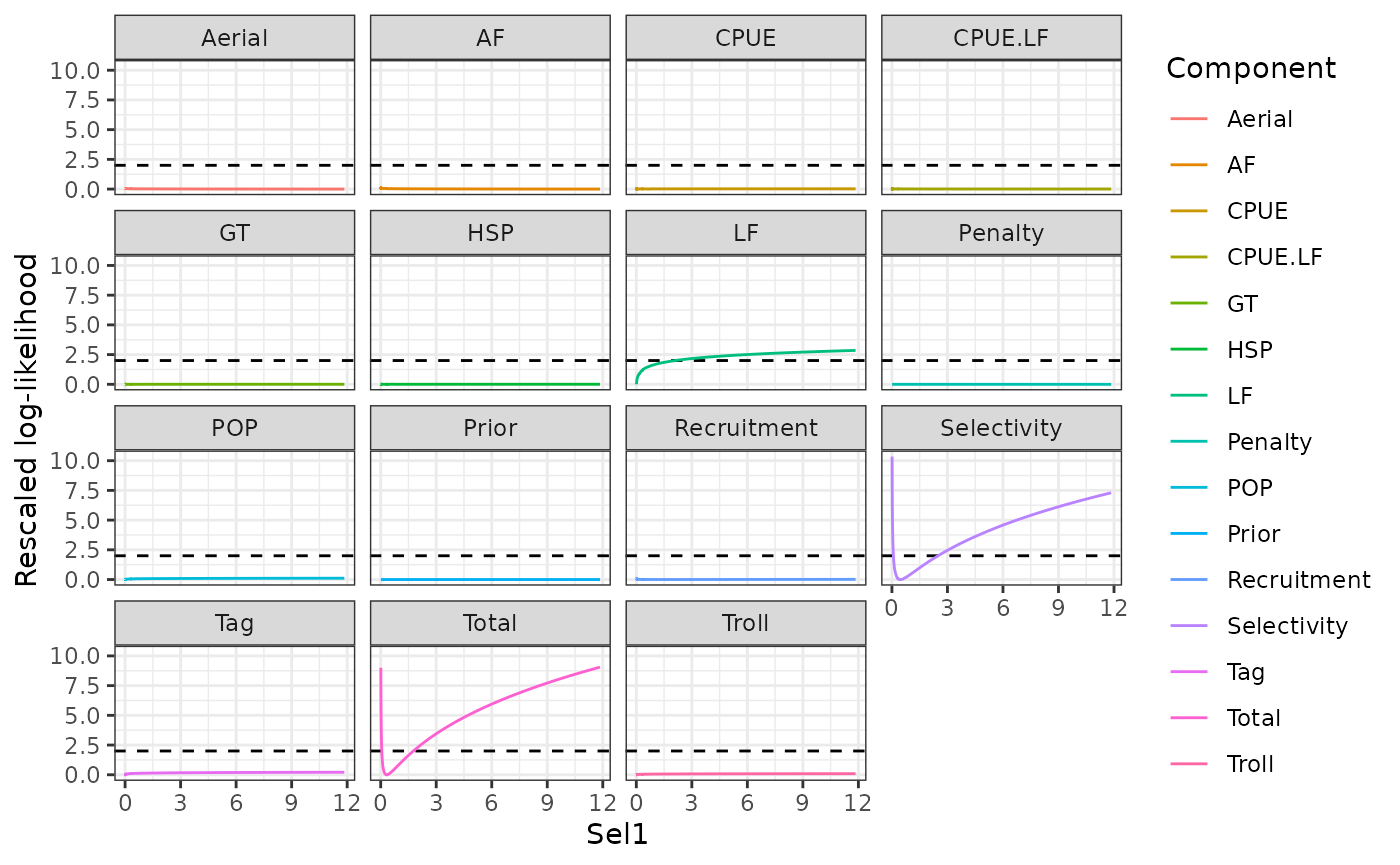

Likelihood profile for one of the selectivity parameters.

Bayesian inference

Bayesian inference can be done using the adnuts package.

library(adnuts)
#> Loading required package: StanEstimators

# mcmc <- sample_snuts(
#   obj = obj, metric = "auto", init = "last.par.best",
#   # lower = bnd$lower, upper = bnd$upper, # these bounds dont seem to work
#   # skip_optimization = TRUE, # Can skip for Jacobians
#   num_samples = 1000, num_warmup = 750, chains = 4, cores = 4,
#   control = list(adapt_delta = 0.99), globals = sbt_globals()
# )
# save(mcmc, file = "mcmc.rda")

load("mcmc.rda")

plot_sampler_params(fit = mcmc, plot = TRUE)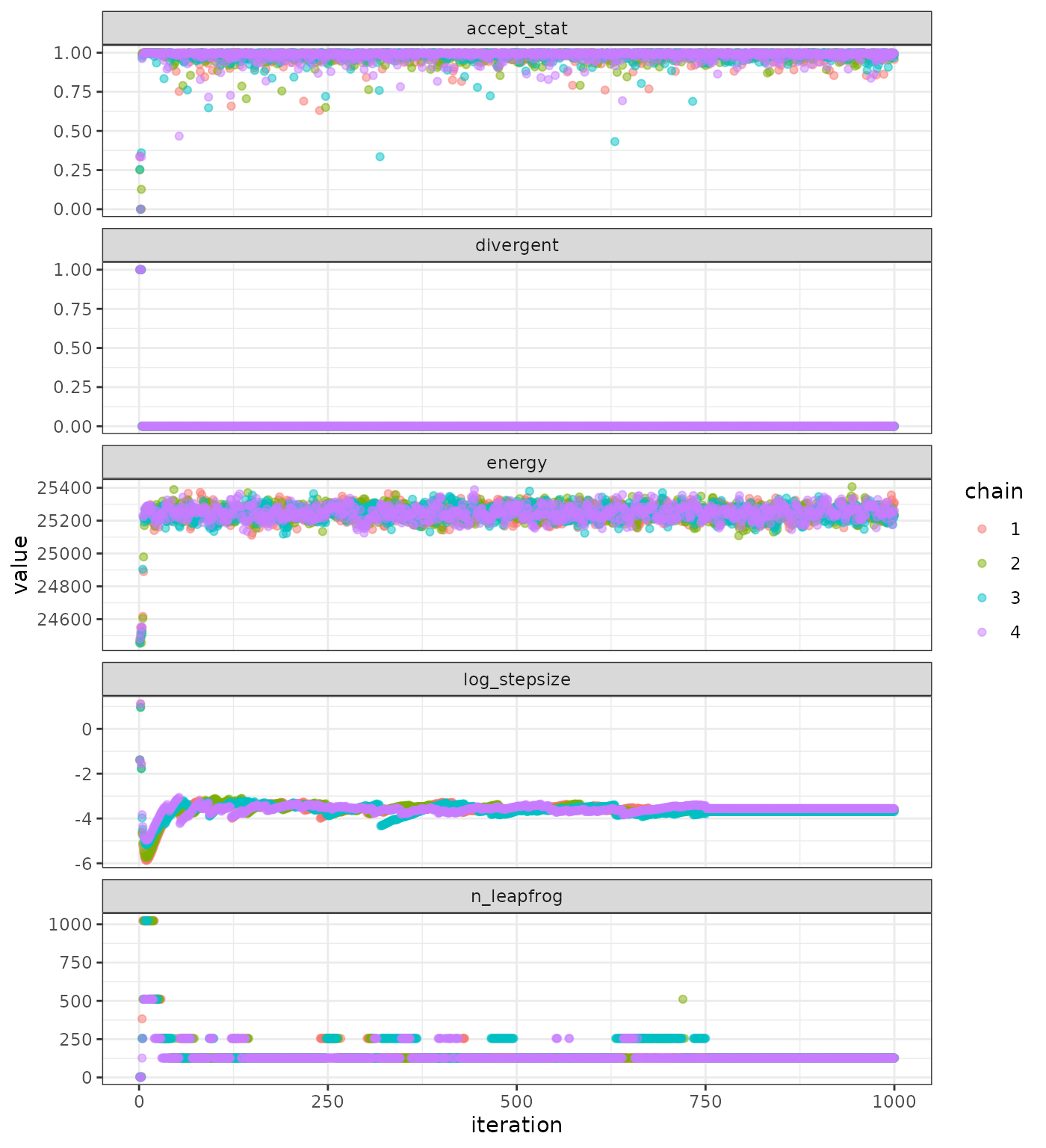

Sampler parameters.

# decamod::pairs_rtmb(fit = mcmc, order = "slow", pars = 1:5)
# decamod::pairs_rtmb(fit = mcmc, order = "mismatch", pars = 1:5)
# decamod::pairs_rtmb(fit = mcmc, order = "fast", pars = 1:5)
plot_uncertainties(fit = mcmc, log = TRUE, plot = TRUE)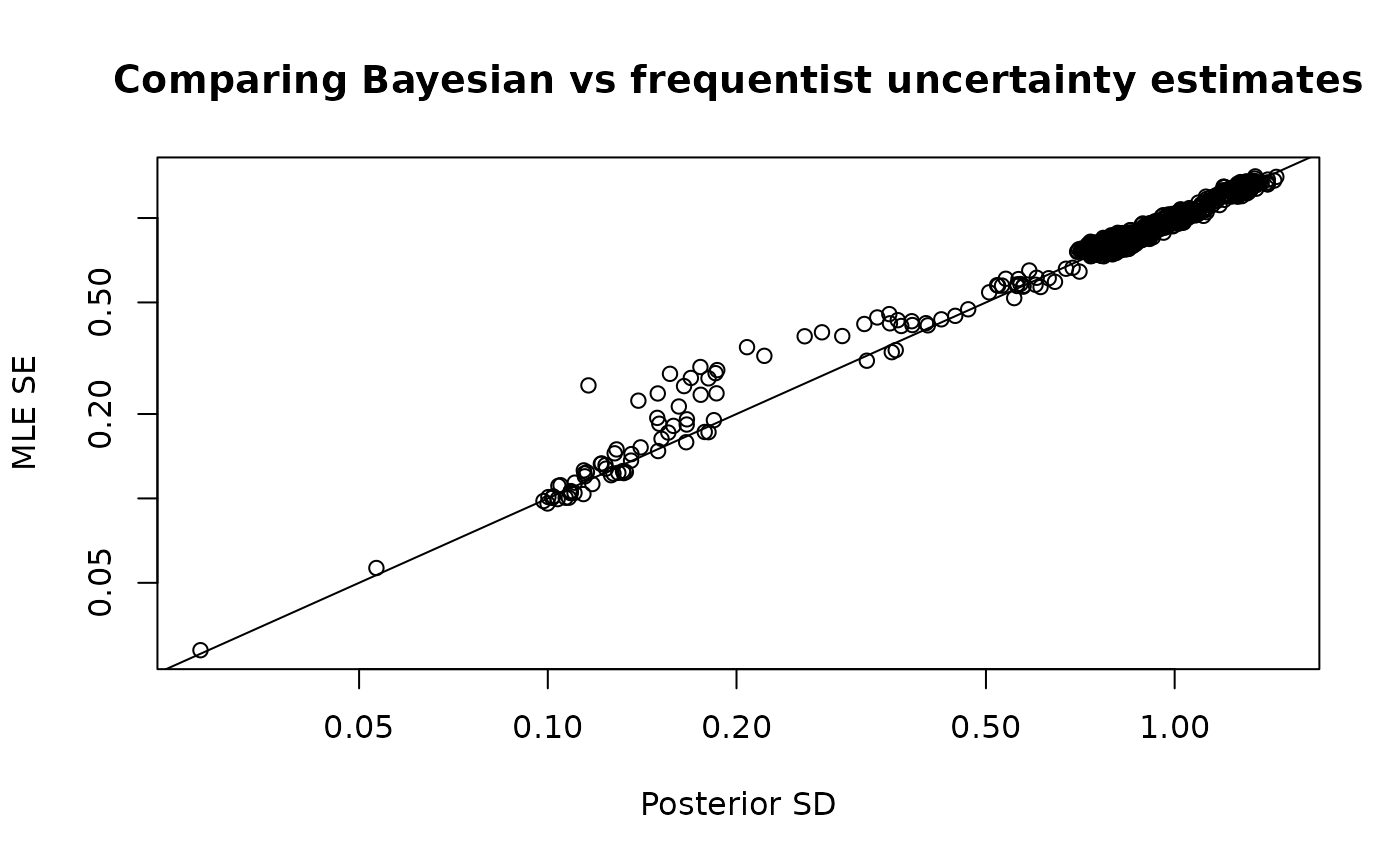

Comparison of Bayesian and frequentist uncertainty estimates.

Projection

Projections can be based on MLE or MCMC.

Recruitment

Recruitment projections can be done the project_recruitment function. Can be done using using Autoregressive Integrated Moving Average (ARIMA) models by setting arima = TRUE.

n_proj <- 10

proj <- project_recruitment(
  data = data, obj = obj, mcmc = NULL, first_yr = 1931, last_yr = 2022, 
  n_proj = n_proj, n_iter = 10, arima = TRUE, max.p = 5)
#>   |                                                                              |                                                                      |   0%  |                                                                              |========                                                              |  11%  |                                                                              |================                                                      |  22%  |                                                                              |=======================                                               |  33%  |                                                                              |===============================                                       |  44%  |                                                                              |=======================================                               |  56%  |                                                                              |===============================================                       |  67%  |                                                                              |======================================================                |  78%  |                                                                              |==============================================================        |  89%  |                                                                              |======================================================================| 100%

plot_rec_devs(data = data, object = obj, proj = proj)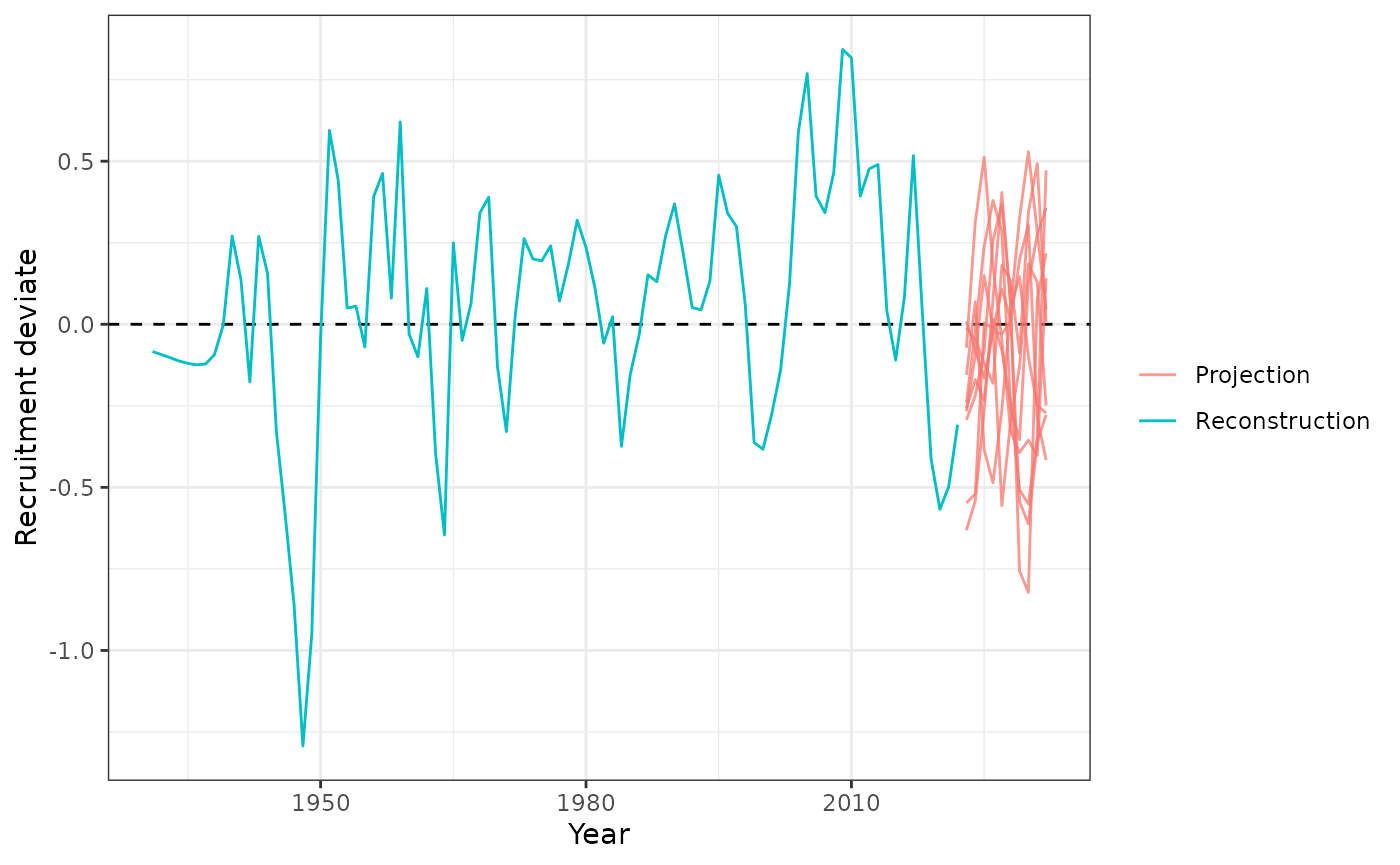

Selectivity

Projecting selectivity can be done using the project_selectivity function. The first_yr and the last_yr arguments define the range of years over which the mean and standard deviation of selectivity is calculated. Future selectivity is then drawn from a normal distribution (in log-space).

proj <- project_selectivity(
  data = data, obj = obj, mcmc = NULL, first_yr = 2015, last_yr = NULL, 
  n_proj = n_proj, n_iter = 100)

df <- reshape2::melt(proj)
ggplot(data = df) +
  geom_line(aes(x = age, y = value, color = factor(year), group = interaction(iteration, year))) +
  facet_wrap(fishery ~ .)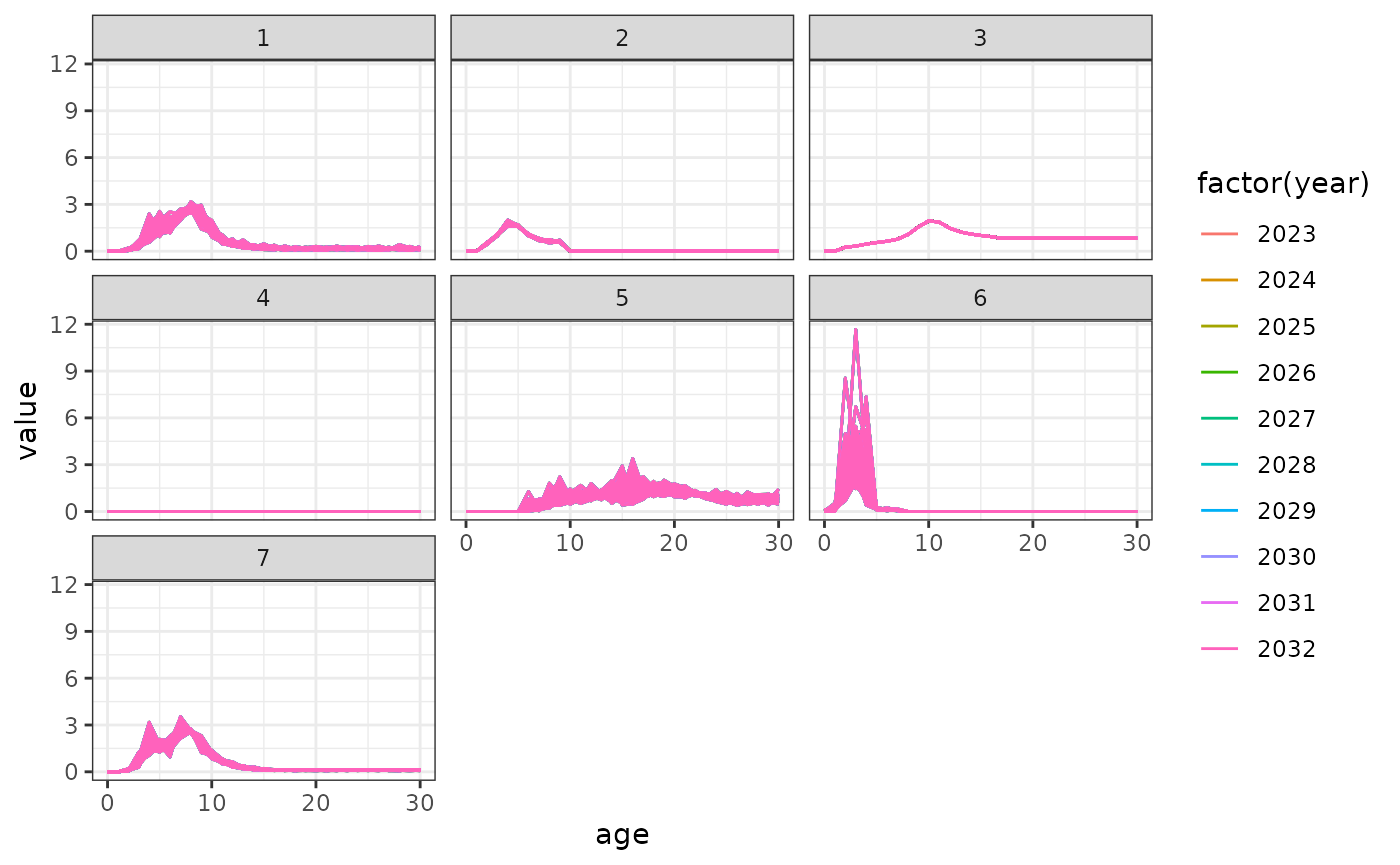

Catch

dim(data$catch_obs_ysf)
#> [1] 71  2  6
dn <- dimnames(data$catch_obs_ysf)
proj_years <- (data$last_yr + 1):(data$last_yr + n_proj)
catch_proj_ysf <- array(0, dim = list(n_proj, 2, 6), dimnames = list(Year = proj_years, Season = dn$Season, Fishery = dn$Fishery))
for (y in 1:n_proj) catch_proj_ysf[y,,] <- data$catch_obs_ysf[71,,]
catch_proj_ysf[1,,]
#>       Fishery
#> Season     LL1     LL2  LL3 LL4 Indonesia Australia
#>      1    0.00    0.00 1.27   0    732.54  5931.804
#>      2 9905.87 1314.67 0.00   0      0.00     0.000

plot_catch(data = data, object = obj, proj = catch_proj_ysf)
#> [1] "The maximum catch difference was: NA"
#> Warning: Removed 10 rows containing missing values or values outside the scale range
#> (`geom_line()`).

References

Kristensen, Kasper. 2024. “RTMB: R Interface to TMB for Fully Symbolic AD Models.” https://github.com/kaskr/RTMB.

Kristensen, Kasper, Anders Nielsen, Casper W. Berg, Hans Skaug, and Bradley M. Bell. 2016. “TMB: Automatic Differentiation and Laplace Approximation.” Journal of Statistical Software 70 (5): 1–21. https://doi.org/10.18637/jss.v070.i05.

R Core Team. 2024. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.